Complément au cours

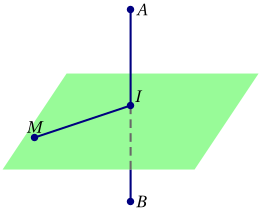
Soit, dans l'espace, un segment $[AB]$. Quel est l'ensemble des points équidistants de $A$ et de $B$?

Notons $I$ le milieu de $[AB]$. Un point $M$ quelconque est équidistant de $A$ et $B$ si et seulement si: \[\begin{aligned} AM &= MB& \\ \iff AM^2 &= BM^2& \\ \iff {\overrightarrow{AM}}^2 &=\overrightarrow{BM}^2& \\ \iff (\overrightarrow{AI}+\overrightarrow{IM})^2 &= (\overrightarrow{BI}+\overrightarrow{IM})^2 \\ \iff \cancel{AI^2} + 2\overrightarrow{AI}\cdot\overrightarrow{IM} + \cancel{IM^2} &= \cancel{BI^2} + 2\overrightarrow{BI}\cdot\overrightarrow{IM} + \cancel{IM^2}& \end{aligned}\] En effet, $I$ étant milieu de $[AB]$, $AI = BI$ donc $AI^2 = BI^2$.
Reprenons en remarquant que $2\overrightarrow{AI} = \overrightarrow{AB}$ et $2\overrightarrow{BI} = \overrightarrow{BA} = -\overrightarrow{AB}$: \[\begin{aligned} {2}\overrightarrow{AI}\cdot\overrightarrow{IM} & = {2}\overrightarrow{BI}\cdot\overrightarrow{IM}& \\ \iff \overrightarrow{AB}\cdot\overrightarrow{IM} & = -\overrightarrow{AB}\cdot\overrightarrow{IM} & \\ \iff \overrightarrow{AB}\cdot\overrightarrow{IM} + \overrightarrow{AB}\cdot\overrightarrow{IM} &=0& \\ \iff 2\overrightarrow{AB}\cdot\overrightarrow{IM} &=0& \\ \iff \overrightarrow{AB}\cdot\overrightarrow{IM} & = 0.& \end{aligned}\] Or cette dernière condition équivaut à demander que le vecteur $\overrightarrow{IM}$ soit orthogonal au vecteur $\overrightarrow{AB}$, soit encore que $M$ soit sur le plan passant par $I$ et de vecteur normal $\overrightarrow{AB}$. Donc:

L'ensemble des points équidistants de $A$ et $B$ est le plan perpendiculaire à $[AB]$ passant par son milieu $I$. Ce plan est appelé plan médiateur du segment $[AB]$.

Exercices par capacité attendue

Calculer un produit scalaire
- En utilisant le projeté orthogonal, un cosinus ou avec les formules de polarisation:
  Savoir-faire n°1 p. 95 11 p. 95 12 p. 95 ex-617 ex-618 ex-619 ex-620 ex-621 ex-622 ex-629 ex-630 ex-632
- Avec les coordonnées dans un repère orthonormé:
  57 p. 106 60 p. 106 61 p. 106 ex-623 ex-627 ex-628
- En utilisant les propriétés "algébriques" du produit scalaire:
  56 p. 106 ex-122 ex-123
Déterminer un vecteur normal à un plan:
50 p. 105 83 p. 108 84 p. 108 ex-409
Utiliser le produit scalaire pour
- Démontrer une orthogonalité:
  57 p. 106 74 p. 108 75 p. 108 76 p. 108 81 p. 108 ex-264 ex-265 ex-288 ex-290 ex-626
- Pour calculer un angle:
  15 p. 99 97 p. 110 99 p. 110 ex-425 ex-426 ex-882
- Pour calculer une longueur dans l’espace:
  96 p. 110 ex-624 ex-625
Utiliser la projection orthogonale pour déterminer la distance d’un point à une droite ou à un plan:
100 p. 110 101 p. 110 104 p. 110
Résoudre des problèmes impliquant des grandeurs et mesures (longueur, angle, aire, volume):
96 p. 110 105 p. 110 108 p. 110 ex-631
Étudier des problèmes de configuration dans l’espace:
- orthogonalité de deux droites:
  74 p. 108 81 p. 108 88 p. 108
- orthogonalité d’une droite et d’un plan:
  76 p. 108 82 p. 108 87 p. 108 ex-289
- lieux géométriques simples, par exemple plan médiateur de deux points.
  ???
Déterminer une représentation paramétrique d’une droite:
70 p. 138
Reconnaître une droite donnée par une représentation paramétrique:
65 p. 138 66 p. 138
Déterminer l’équation cartésienne d’un plan dont on connaît un vecteur normal et un point:
47 p. 136 53 p. 136
Reconnaître un plan donné par une équation cartésienne et préciser un vecteur normal à ce plan:
46 p. 136
Déterminer les positions relatives
ex-651
- de deux droites:
  66 p. 138 ex-883
- d'une droite et d'un plan:
  69 p. 138
- de deux plans:
  48 p. 136
Déterminer les coordonnées du projeté orthogonal [...]
79 p. 140 80 p. 140 81 p. 140 82 p. 140
Dans un cadre géométrique repéré, traduire par un système d’équations linéaires des problèmes de types suivants:
- décider si trois vecteurs forment une base:
  ???
- déterminer les coordonnées d’un vecteur dans une base
  ???
- étudier une configuration dans l’espace (alignement, colinéarité, parallélisme, coplanarité, intersection et orthogonalité de droites ou de plans), etc.:
  71 p. 138 72 p. 138

Exercices bilans, types bac, approfondissements

ex-110 ex-111 ex-796 (bac) ex-800 (bac) ex-806 (bac) ex-813 (bac) ex-818 (bac)

retour