retour

Soit le cube $ABCDEFGH$ d'arête $a$ (où $a\in\mathbb R^+_*$) représenté ci-dessous.

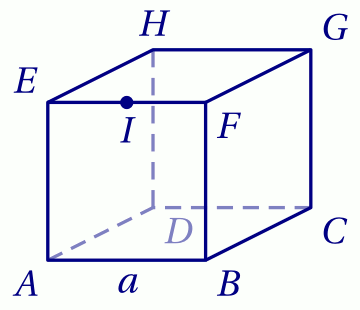
$I$ est le milieu de l'arête $[EF]$.

Exprimer en fonction de $a$ les produits scalaires suivants.

1. $\overrightarrow{AB}\cdot\overrightarrow{AB}$;    Corrigé
   $\overrightarrow{AB}\cdot\overrightarrow{AB} = (\overrightarrow{AB})^2=a^2$.
2. $\overrightarrow{AB}\cdot\overrightarrow{AC}$;    Corrigé
   $C$ se projette orthogonalement sur $(AB)$ en $B$ donc: \[\overrightarrow{AB}\cdot\overrightarrow{AC} = \overrightarrow{AB}\cdot\overrightarrow{AB} = a^2.\]
3. $\overrightarrow{AB}\cdot\overrightarrow{AG}$;    Corrigé
   $G$ se projette aussi orthogonalement sur $(AB)$ en $B$ donc: \[\overrightarrow{AB}\cdot\overrightarrow{AG} = \overrightarrow{AB}^2 = a^2.\]
4. $\overrightarrow{AB}\cdot\overrightarrow{AD}$;    Corrigé
   $\overrightarrow{AB}\perp\overrightarrow{AD}$ donc $\overrightarrow{AB}\cdot\overrightarrow{AD}=0$.
5. $\overrightarrow{AB}\cdot\overrightarrow{AI}$;    Corrigé
   $I$ se projette orthogonalement sur $(AB)$ au milieu de $[AB]$ donc : \[\overrightarrow{AB}\cdot\overrightarrow{AI} = \overrightarrow{AB}\cdot \frac 1 2 \overrightarrow{AB} =\frac 1 2 \overrightarrow{AB}^2 = \frac{a^2} 2.\]
6. $\overrightarrow{IA}\cdot\overrightarrow{IB}$.    Corrigé
   On a : \begin{align*} \overrightarrow{IA}\cdot\overrightarrow{IB} &=\left(\overrightarrow{IE}+\overrightarrow{EA}\right)\cdot\left(\overrightarrow{IF}\cdot\overrightarrow{FB}\right)& \\ &=\left(-\frac 1 2\overrightarrow{AB}+\overrightarrow{EA}\right)\cdot \left(\frac 1 2\overrightarrow{AB}+\overrightarrow{EA}\right)& \\ &=-\frac 1 4\overrightarrow{AB}^2 -\frac 1 2\overrightarrow{AB}\cdot\overrightarrow{EA} +\frac 1 2\overrightarrow{AB}\cdot\overrightarrow{EA} +\overrightarrow{EA}^2& \\ &=-\frac 1 4 a^2 + a^2 = \frac 3 4 a^2.& \end{align*}

retour

code : 629