ex-290
retour
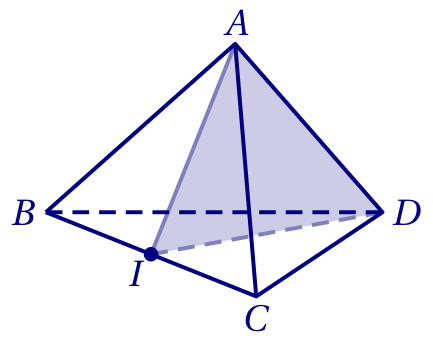
$ABCD$ est un tétraèdre régulier (donc toutes ses faces sont des triangles équilatéraux) et $I$ est le milieu de l'arête $[BC]$.
1.
Démontrer que le vecteur $\overrightarrow{BC}$ est normal au plan $(IAD)$.
Corrigé
Dans le triangle $ABC$, la droite $(AI)$ passe par le sommet $A$ et le milieu du côté $[BC]$.
C'est donc une médiane. Mais le triangle $ABC$ est équilatéral, donc cette médiane est aussi une médiatrice et :
\[\overrightarrow{AI}\perp \overrightarrow{BC}.\]
Dans le triangle $BDC$, la droite $(DI)$ est aussi une médiane, et puisque ce triangle est aussi équilatéral,
cette médiane est aussi une médiatrice. Donc :
\[\overrightarrow{DI}\perp \overrightarrow{BC}.\]
Le vecteur $\overrightarrow{BC}$, orthogonal à la base $(\overrightarrow{AI},\overrightarrow{DI})$ du plan
$(IAD)$ est donc normal à ce plan.
2.
En déduire que les arêtes $[BC]$ et $[AD]$ sont orthogonales.
Corrigé
Le vecteur $\overrightarrow{BC}$ est normal au plan $(IAD)$, donc orthogonal à tout vecteur formé avec
les points de ce plan, donc en particulier au vecteur $\overrightarrow{AD}$.
Les droites $(BC)$ et $(AD)$ que ces vecteurs dirigent sont donc orthogonales.
Les droites $(BC)$ et $(AD)$ que ces vecteurs dirigent sont donc orthogonales.
retour
code : 290