retour
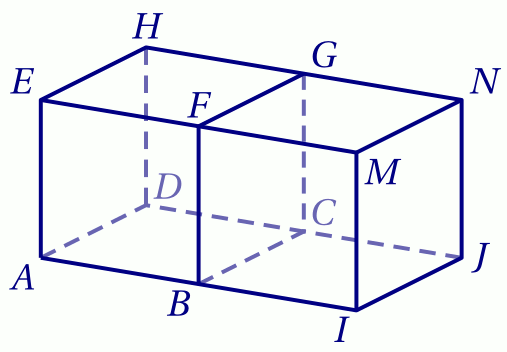
$AIJDEMNH$ est un pavé droit composé de deux cubes accolés de côté $a$.
Calculer les produits scalaires suivants :
1.
$\overrightarrow{AB}\cdot\overrightarrow{AC}$;
Corrigé
$C$ se projette orthogonalement sur $(AB)$ en $B$ donc
\[\overrightarrow{AB}\cdot\overrightarrow{AC} = \overrightarrow{AB}\cdot\overrightarrow{AB} = AB^2 = a^2.\]
2.
$\overrightarrow{BA}\cdot\overrightarrow{BI}$;
Corrigé
$\overrightarrow{BA}$ et $\overrightarrow{BI}$ sont colinéaires de sens contraires donc:
\[\overrightarrow{BA}\cdot\overrightarrow{BI} = -BA\times BI = -a^2.\]
3.
$\overrightarrow{EF}\cdot\overrightarrow{HN}$;
Corrigé
$\overrightarrow{EF}$ et $\overrightarrow{HN}$ sont colinéaires et de même sens donc:
\[\overrightarrow{EF}\cdot\overrightarrow{HN} = EF\times HN = a\times 2a = 2a^2.\]
4.
$\overrightarrow{HF}\cdot\overrightarrow{EG}$;
Corrigé
Les diagonales du carré $EHGF$ sont perpendiculaires, donc les vecteurs $\overrightarrow{HF}$ et $\overrightarrow{EG}$ sont orthogonaux. Donc:
\[\overrightarrow{HF}\cdot\overrightarrow{EG} = 0.\]
5.
$\overrightarrow{EN}\cdot\overrightarrow{EF}$;
Corrigé
Le point $N$ se projette orthogonalement sur $(EF)$ en $M$. Donc :
\[\overrightarrow{EF}\cdot\overrightarrow{EN} = \overrightarrow{EF}\cdot\overrightarrow{EM} = EF\times EM = a\times 2a = 2a^2.\]
6.
$\overrightarrow{AJ}\cdot\overrightarrow{CD}$;
Corrigé
D'abord :
\[\overrightarrow{AJ}\cdot\overrightarrow{CD} = \overrightarrow{AJ}\cdot\overrightarrow{BA} = -\overrightarrow{AJ}\cdot\overrightarrow{AB}.\]
De plus, $J$ se projette orthogonalement sur $(AB)$ en $I$ donc:
\[-\overrightarrow{AJ}\cdot\overrightarrow{AB} = -AI\times AB -2a\times a = -2a^2.\]
7.
$\overrightarrow{AN}\cdot\overrightarrow{AJ}$;
Corrigé
$N$ se projette orthogonalement sur $(AJ)$ en $J$ donc:
\[\overrightarrow{AN}\cdot\overrightarrow{AJ} = \overrightarrow{AJ}\cdot\overrightarrow{AJ} = AJ^2.\]
On peut alors calculer $AJ^2$ à l'aide du théorème de Pythagore, ou de manière équivalente, calculer comme suit.
\[\begin{aligned}
\overrightarrow{AJ}^2 &= (\overrightarrow{AI}+\overrightarrow{IJ})^2&
\\
&=\overrightarrow{AI}^2 + 2\overrightarrow{AI}\cdot\overrightarrow{IJ} + \overrightarrow{IJ}^2&
\\
&=(2a)^2 + 2\times 0 + a^2&
\\
&= 5a^2.&
\end{aligned}\]
8.
$\overrightarrow{CF}\cdot\overrightarrow{AH}$;
Corrigé
$\overrightarrow{CF}=\overrightarrow{DE}$ et les vecteurs $\overrightarrow{DE}$ et $\overrightarrow{AH}$ sont orthogonaux (diagonales d'un carré). Donc:
\[\overrightarrow{CF}\cdot\overrightarrow{AH} = 0.\]
9.
$\overrightarrow{MA}\cdot\overrightarrow{CD}$.
Corrigé
Puisque $\overrightarrow{CD} = \overrightarrow{MF}$ et que $A$ se projette orthogonalement sur $(MF)$ en $A$:
\[\overrightarrow{MA}\cdot\overrightarrow{CD} = \overrightarrow{MA}\cdot\overrightarrow{MF} = ME\times MF = 2a\times a = 2a^2.\]
retour