ex-632
retour
$SABCD$ est une pyramide de base carrée $ABCD$ et de sommet $S$, telle que les faces latérales $SAB$, $SBC$, $SCD$ et $SDA$ sont toutes des triangles équilatéraux.
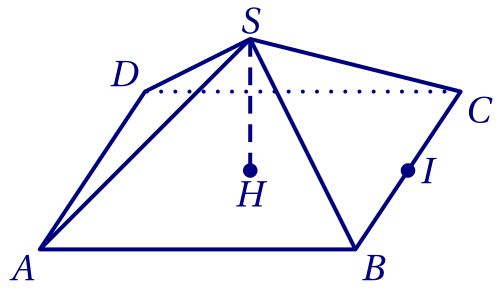
$H$ est le centre du carré $ABCD$ et $I$ est le milieu de $[BC]$. On a de plus $AB=4$.
Calculer, en justifiant, les produits scalaires suivants :
1. $\overrightarrow{SA}\cdot\overrightarrow{SB}$; Corrigé
$SAB$ est équilatéral donc $SA=SB=AB=4$ et $\widehat{ASB} = 60^\circ$. Alors :
\[\overrightarrow{SA}\cdot\overrightarrow{SB} = SA\times SB \times \cos\left(\widehat{ASB}\right)
= 4 \times 4 \times \frac 1 2 = 8.\]
2. $\overrightarrow{AH}\cdot\overrightarrow{DB}$; Corrigé
Les diagonales du carré $ABCD$ sont perpendiculaires donc $\overrightarrow{AH}\perp\overrightarrow{DB}$ et
\[\overrightarrow{AH}\cdot\overrightarrow{DB} = 0.\]
3. $\overrightarrow{SH}\cdot\overrightarrow{AC}$; Corrigé
Le triangle $SAC$ est isocèle en $S$, donc $(SH)$, la médiane issue de $S$ est aussi une médiatrice.
Donc : \[\overrightarrow{SH}\perp\overrightarrow{AC} \implies \overrightarrow{SH}\cdot \overrightarrow{AC} = 0.\]
Donc : \[\overrightarrow{SH}\perp\overrightarrow{AC} \implies \overrightarrow{SH}\cdot \overrightarrow{AC} = 0.\]
4. $\overrightarrow{HI}\cdot\overrightarrow{SC}$. Corrigé
$(SH)$ est la médiane issue de $S$ du triangle $SBD$ et ce triangle est isocèle en $S$,
donc $(SH)$ est perpendiculaire à $(BD)$.
Donc $\overrightarrow{HS}$, orthogonal à la fois à $\overrightarrow{AC}$ et $\overrightarrow{BD}$, est normal au plan $(ABC)$.
Il est donc en particulier orthogonal au vecteur $\overrightarrow{HI}$.
D'autre part, dans le triangle $CAB$, $I$ est le milieu de $[CB]$ et $H$ celui de $[CA]$. Alors : \begin{align*} \overrightarrow{IH} &= \overrightarrow{IC}+\overrightarrow{CH} =\frac 1 2 \overrightarrow{BC}+\frac 1 2\overrightarrow{CA} =\frac 1 2 (\overrightarrow{BC}+\overrightarrow{CA})& \\ &=\frac 1 2 \overrightarrow{BA}.& \end{align*} Donc $IH = 2$ et $\overrightarrow{IH}\perp\overrightarrow{IC}$. Enfin : \begin{align*} \overrightarrow{HI}\cdot\overrightarrow{SC} &=\overrightarrow{HI}\cdot(\overrightarrow{SI}+\overrightarrow{IC}) =\overrightarrow{HI}\cdot\overrightarrow{SI} +\underbrace{\overrightarrow{HI}\cdot\overrightarrow{IC}}_{\overrightarrow{HI}\perp\overrightarrow{IC}}& \\ &=(-\overrightarrow{IH})\cdot(-\overrightarrow{IS}) + 0 =\overrightarrow{IH}\cdot\overrightarrow{IS}& \\ &=\overrightarrow{IH}\cdot(\overrightarrow{IH}+\overrightarrow{HS}) =\overrightarrow{IH}^2 + \underbrace{\overrightarrow{IH}\cdot\overrightarrow{HS}}_{\overrightarrow{IH}\perp\overrightarrow{HS}}& \\ &=IH^2 =2^2 =4.& \end{align*}
Donc $\overrightarrow{HS}$, orthogonal à la fois à $\overrightarrow{AC}$ et $\overrightarrow{BD}$, est normal au plan $(ABC)$.
Il est donc en particulier orthogonal au vecteur $\overrightarrow{HI}$.
D'autre part, dans le triangle $CAB$, $I$ est le milieu de $[CB]$ et $H$ celui de $[CA]$. Alors : \begin{align*} \overrightarrow{IH} &= \overrightarrow{IC}+\overrightarrow{CH} =\frac 1 2 \overrightarrow{BC}+\frac 1 2\overrightarrow{CA} =\frac 1 2 (\overrightarrow{BC}+\overrightarrow{CA})& \\ &=\frac 1 2 \overrightarrow{BA}.& \end{align*} Donc $IH = 2$ et $\overrightarrow{IH}\perp\overrightarrow{IC}$. Enfin : \begin{align*} \overrightarrow{HI}\cdot\overrightarrow{SC} &=\overrightarrow{HI}\cdot(\overrightarrow{SI}+\overrightarrow{IC}) =\overrightarrow{HI}\cdot\overrightarrow{SI} +\underbrace{\overrightarrow{HI}\cdot\overrightarrow{IC}}_{\overrightarrow{HI}\perp\overrightarrow{IC}}& \\ &=(-\overrightarrow{IH})\cdot(-\overrightarrow{IS}) + 0 =\overrightarrow{IH}\cdot\overrightarrow{IS}& \\ &=\overrightarrow{IH}\cdot(\overrightarrow{IH}+\overrightarrow{HS}) =\overrightarrow{IH}^2 + \underbrace{\overrightarrow{IH}\cdot\overrightarrow{HS}}_{\overrightarrow{IH}\perp\overrightarrow{HS}}& \\ &=IH^2 =2^2 =4.& \end{align*}
retour
code : 632