ex-620
retour
$ABCD$ est un un tétraèdre régulier de côté $a$ (toutes ses arêtes mesurent $a$).
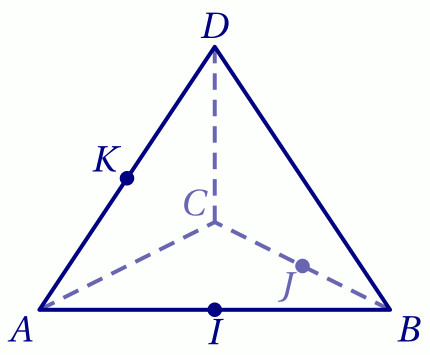
$I$, $J$ et $K$ sont les milieux respectifs des arêtes $[AB]$, $[BC]$ et $[AD]$.
Exprimer en fonction de $a$ les produits scalaires suivants :
1. $\overrightarrow{DA}\cdot\overrightarrow{DB}$; Corrigé
$DAB$ est un triangle équilatéral donc $\widehat{ADB} = 60°$.
\[\overrightarrow{DA}\cdot\overrightarrow{DB}
= DA\times DB \times \cos 60°
=\frac 1 2 a^2.\]
2. $\overrightarrow{AK}\cdot\overrightarrow{DI}$; Corrigé
Dans le triangle équilatéral $DAB$, la médiane $[DI]$ est aussi une hauteur.
Le triangle $ADI$ est donc rectangle en $I$ et \[\begin{aligned} AI^2 + DI^2 &= AD^2& \\ \implies DI^2 &= AD^2 - AI^2& \\ \implies DI^2 &= a^2 - \left(\frac 1 2 a\right)^2& \\ \implies DI^2 &= a^2 - \frac 1 4 a^2& \\ \implies DI^2&= \frac 3 4 a^2.& \end{aligned}\] On en déduit aussi que le projeté orthogonal de $A$ sur $(DI)$ est $I$.
Finalement \[\begin{aligned} \overrightarrow{AK}\cdot\overrightarrow{DI} &= -\frac 1 2\overrightarrow{DA}\cdot\overrightarrow{DI}& \\ &=-\frac 1 2 \overrightarrow{DI}\cdot\overrightarrow{DI}& \\ &=-\frac 1 2 DI^2& \\ &=-\frac 1 2 \times \frac 3 4 a^2& \\ &=-\frac 3 8 a^2.& \end{aligned}\]
Le triangle $ADI$ est donc rectangle en $I$ et \[\begin{aligned} AI^2 + DI^2 &= AD^2& \\ \implies DI^2 &= AD^2 - AI^2& \\ \implies DI^2 &= a^2 - \left(\frac 1 2 a\right)^2& \\ \implies DI^2 &= a^2 - \frac 1 4 a^2& \\ \implies DI^2&= \frac 3 4 a^2.& \end{aligned}\] On en déduit aussi que le projeté orthogonal de $A$ sur $(DI)$ est $I$.
Finalement \[\begin{aligned} \overrightarrow{AK}\cdot\overrightarrow{DI} &= -\frac 1 2\overrightarrow{DA}\cdot\overrightarrow{DI}& \\ &=-\frac 1 2 \overrightarrow{DI}\cdot\overrightarrow{DI}& \\ &=-\frac 1 2 DI^2& \\ &=-\frac 1 2 \times \frac 3 4 a^2& \\ &=-\frac 3 8 a^2.& \end{aligned}\]
3. $\overrightarrow{IK}\cdot\overrightarrow{AC}$; Corrigé
\[\begin{aligned}
\overrightarrow{IK}\cdot\overrightarrow{AC}
&=(\overrightarrow{IC}+\overrightarrow{CK})\cdot\overrightarrow{AC}&
\\
&=\overrightarrow{IC}\cdot\overrightarrow{AC} + \overrightarrow{CK}\cdot\overrightarrow{AC}&
\\
&=(-\overrightarrow{CI})\cdot(-\overrightarrow{CA}) + \overrightarrow{CK}\cdot(-\overrightarrow{AC})&
\\
&=\overrightarrow{CI}\cdot\overrightarrow{CA} - \overrightarrow{CK}\overrightarrow{CA}&
\end{aligned}\]
$A$ se projette orthogonalement sur $(CI)$ en $I$ et sur $(CK)$ en $K$. Donc :
\[\begin{aligned}
\overrightarrow{IK}\cdot\overrightarrow{AC}
&=\overrightarrow{CI}\cdot\overrightarrow{CA} - \overrightarrow{CK}\overrightarrow{CA}&
\\
&=CI^2 - CK^2&
\\
&=0.&
\end{aligned}\]
(Car $CI = CK$.)
4. $\overrightarrow{JK}\cdot\overrightarrow{AD}$. Corrigé
\[\begin{aligned}
\overrightarrow{JK}\cdot\overrightarrow{AD}
&=(\overrightarrow{JC}+\overrightarrow{CK})\cdot\overrightarrow{AD}&
\\
&=\overrightarrow{JC}\cdot\overrightarrow{AD} + \underbrace{\overrightarrow{CK}\cdot\overrightarrow{AD}}_{\overrightarrow{CK}\perp\overrightarrow{AD}}&
\\
&=\overrightarrow{JC}\cdot\overrightarrow{AD} + 0&
\\
&=\overrightarrow{JC}\cdot(\overrightarrow{AB}+\overrightarrow{BD})&
\\
&=\overrightarrow{JC}\cdot\overrightarrow{AB} + \overrightarrow{JC}\cdot\overrightarrow{BD}&
\\
&=\frac 1 2\overrightarrow{BC}\cdot(-\overrightarrow{BA}) + \frac 1 2 \overrightarrow{BC}\cdot\overrightarrow{BD}&
\\
&=-\frac 1 2 \times \frac 1 2 a^2 + \frac 1 2 \times \frac 1 2 a^2&
\\
&=0.&
\end{aligned}\]
retour
code : 620