retour
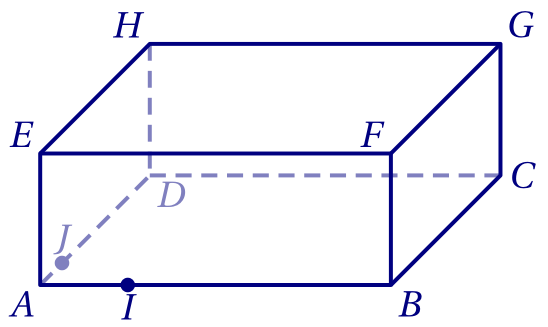
On a représenté ci-dessous le pavé droit $ABCDEFGH$ tel que
\[AB = 8,\quad AD=5\quad\text{et}\quad AE = 3.\]
Les points $I$ et $J$ sont définis par
\[\overrightarrow{AI} = \frac 1 4 \overrightarrow{AB} \quad\text{et}\quad \overrightarrow{AJ} = \frac 2 5 \overrightarrow{AD}.\]
1.
Calculer les produits scalaires suivants :
a.
$\overrightarrow{AI}\cdot\overrightarrow{AB}$;
Corrigé
$\overrightarrow{AI}$ et $\overrightarrow{AB}$ sont colinéaires de même sens donc:
\[\overrightarrow{AI}\cdot\overrightarrow{AB} = AI\times AB = 2\times 8 = 16.\]
b.
$\overrightarrow{AB}\cdot\overrightarrow{DH}$;
Corrigé
$\overrightarrow{AB}$ et $\overrightarrow{DH}$ sont orthogonaux donc:
\[\overrightarrow{AB}\cdot\overrightarrow{DH} = 0.\]
c.
$\overrightarrow{EH}\cdot\overrightarrow{CB}$;
Corrigé
$\overrightarrow{EH}$ et $\overrightarrow{CB}$ sont colinéaires de sens contraires, donc:
\[\overrightarrow{EH}\cdot\overrightarrow{CB} = -EH\times CB = -5^2 = -25.\]
d.
$\overrightarrow{AB}\cdot\overrightarrow{AC}$;
Corrigé
$C$ se projette orthogonalement sur la droite $(AB)$ en $B$ donc:
\[\overrightarrow{AB}\cdot\overrightarrow{AC} = \left(\overrightarrow{AB}\right)^2
= AB^2 = 8^2 = 64.\]
e.
$\overrightarrow{AJ}\cdot\overrightarrow{EF}$;
Corrigé
$\overrightarrow{AJ}$ et $\overrightarrow{EF}$ sont orthogonaux donc:
\[\overrightarrow{AJ}\cdot\overrightarrow{EF} = 0.\]
f.
$\overrightarrow{BI}\cdot\overrightarrow{BD}$.
Corrigé
$D$ se projette orthogonalement sur $(AB)$ en $A$ donc:
\[\overrightarrow{BI}\cdot\overrightarrow{BD}
=\overrightarrow{BI}\cdot\overrightarrow{BA}
=BI\times BA = 6\times 8 = 48.\]
2.
Calculer le produit scalaire $\overrightarrow{JI}\cdot\overrightarrow{JC}$.
Corrigé
Décomposons ces vecteurs selon les directions des arêtes du pavé droit.
\begin{align*}
\overrightarrow{JI}\cdot\overrightarrow{JC}
&=(\overrightarrow{JA}+\overrightarrow{AI})\cdot(\overrightarrow{JD}+\overrightarrow{DC})&
\\
&=\overrightarrow{JA}\cdot\overrightarrow{JD} + \overrightarrow{JA}\cdot\overrightarrow{DC}
+\overrightarrow{AI}\cdot\overrightarrow{JD} + \overrightarrow{AI}\cdot\overrightarrow{DC}&
\\
&=-JA\times JD + 0 + 0 + AI \times DC&
\\
&=-2\times 3 + 2\times 8&
\\
&=10.&
\end{align*}
3.
En déduire une mesure arrondie au degré près de l'angle $\widehat{IJC}$.
Corrigé
Calculons les longueurs $JI$ et $JC$:
\begin{align*}
JI^2 = \overrightarrow{JI}^2 &= (\overrightarrow{JA}+\overrightarrow{AI})^2&
\\
&=\overrightarrow{JA}^2 + 2\overrightarrow{JA}\cdot\overrightarrow{AI} + \overrightarrow{AI}^2&
\\
&=JA^2 + 0 + AI^2&
\\
&=2^2 + 2^2&
\\
&=8.&
\end{align*}
Donc $JI = \sqrt{8} = 2\sqrt 2$.
\begin{align*}
JC^2 = \overrightarrow{JC}^2 &= (\overrightarrow{JD}+\overrightarrow{DC})^2&
\\
&=\overrightarrow{JD}^2 + 2\overrightarrow{JD}\cdot\overrightarrow{DC} + \overrightarrow{DC}^2&
\\
&=JD^2 + 0 + DC^2&
\\
&=3^2 + 8^2&
\\
&=73.&
\end{align*}
Donc $JC = \sqrt{73}$.
Or
\begin{align*}
JI \times JC \times \cos\widehat{IJC} &= \overrightarrow{JI}\cdot\overrightarrow{JC}&
\\ \iff
2\sqrt{2} \times \sqrt{73} \times \cos\widehat{IJC} &= 10&
\\ \iff
\cos\widehat{IJC} &=\frac{10}{2\sqrt{2}\sqrt{73}}&
\\ \iff
\cos\widehat{IJC} &=\frac{5}{\sqrt{146}}.&
\\ \implies
\widehat{IJC} &= \arccos\frac{5}{\sqrt{146}}.&
\end{align*}
Ce qui, selon la calculatrice, conduit à $\widehat{IJC}\approx 66°$.
retour