ex-806

retour

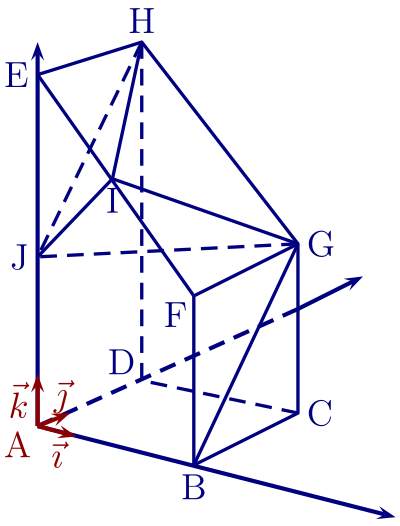
On considère le prisme droit $\mathrm{ABFEDCGH}$, de base $\mathrm{ABFE}$, trapèze rectangle en $\mathrm A$.
On associe à ce prisme le repère orthonormé $\left(\mathrm{A};\vec{\imath},\vec{\jmath},\vec{k}\right)$ tel que : \[\vec{\imath} = \dfrac14\overrightarrow{\mathrm{AB}},\ \vec{\jmath} = \dfrac14\overrightarrow{\mathrm{AD}}, \ \vec{k} = \dfrac18\overrightarrow{\mathrm{AE}}.\] De plus on a $\overrightarrow{\text{BF}} = \dfrac12\overrightarrow{\text{AE}}$.
On note $\mathrm I$ le milieu du segment $[\mathrm{EF}]$.
On note $\mathrm J$ le milieu du segment $[\mathrm{AE}]$.

1. Donner les coordonnées des points $\mathrm I$ et $\mathrm J$.
Corrigé

Le point $\mathrm E$ a pour coordonnées $\left(0;0;8\right)$ et le point $\mathrm F$ a pour coordonnées $(4;0;4)$.
Donc le point $I$ a pour coordonnées \[\left(\frac{0+4}2;\frac{0+0}2;\frac{8+4}2\right) = \left(2;0;,6\right).\] De même, le point $\mathrm A$ a pour coordonnées $\left(0;0;0\right)$ donc le point $\mathrm J$ a pour coordonnées \[\left(\frac{0+0}2;\frac{0+0}2;\frac{0+8}2\right) = \left(0;0;4\right).\]

2. Soit $\vec{n}$ le vecteur de coordonnées $\begin{pmatrix}-1\\1\\1\end{pmatrix}$.

a. Montrer que le vecteur $\vec{n}$ est normal au plan $(\mathrm{IGJ})$.
Corrigé

Le point $\mathrm G$ a pour coordonnées $(4;4;4)$. Donc $\overrightarrow{\mathrm{IG}}$ a pour coordonnées \[\begin{pmatrix}4-2\\4-0\\4-6\end{pmatrix} = \begin{pmatrix}2\\4\\-2\end{pmatrix}.\] De même, le vecteur $\overrightarrow{\mathrm{IJ}}$ a pour coordonnées \[\begin{pmatrix}0-2\\0-0\\4-6\end{pmatrix}=\begin{pmatrix}-2\\0\\-2\end{pmatrix}.\] Donc : \[\begin{aligned} &\vec n \cdot\overrightarrow{\mathrm{IG}} =-1\times 2 + 1\times 4 + 1\times (-2) = 0\;;& \\ &\vec n \cdot \overrightarrow{\mathrm{IJ}} =-1\times(-2) + 1\times 0 + 1\times (-2) = 0.& \end{aligned}\] Donc $\vec n$ est orthogonal aux deux vecteurs d'une base de $(\mathrm{IGJ})$. Il est donc normal à ce plan.

2.b. Déterminer une équation cartésienne du plan $(\mathrm{IGJ})$.
Corrigé

Puisque $\vec n\begin{pmatrix}-1\\1\\1\end{pmatrix}$ est normal au plan $(\mathrm{IGJ})$, ce dernier admet une équation cartésienne de la forme \[-x + y + z + d = 0\] où $d$ est une constante réelle à déterminer.
Puisque $\mathrm J$ est sur ce plan, ses coordonnées en vérifient l'équation: \[\begin{aligned} &-x_{\mathrm J} + y_{\mathrm J} + z_{\mathrm J} + d = 0& \\ \iff &-0 + 0 + 4 + d = 0& \\ \iff &d = -4.& \end{aligned}\] Donc: \[(\mathrm{IGJ}):\quad -x + y + z - 4 = 0.\]

3. Déterminer une représentation paramétrique de la droite $d$, perpendiculaire au plan $(\mathrm{IGJ})$ et passant par $\mathrm H$.
Corrigé

Puisque $d$ est perpendiculaire au plan $(\mathrm{IGJ})$, $\vec n\begin{pmatrix}-1\\1\\1\end{pmatrix}$ dirige $d$. On sait de plus qu'elle passe par le point $\mathrm H(0;4;8)$.
Donc elle admet pour représentation paramétrique \[d:\quad\begin{cases}x=-t\\y=t+4\\z=t+8\end{cases}(t\in\mathbb R).\]

4. On note $\mathrm L$ le projeté orthogonal du point $\mathrm H$ sur le plan $(\mathrm{IGJ})$. Montrer que les coordonnées de $\mathrm L$ sont $\left(\dfrac83;\dfrac43;\dfrac{16}{3}\right)$.
Corrigé

$\mathrm L$ appartient à la droite $d$, donc il existe un réel $t$ pour lequel \[x_{\mathrm L}=-t,\quad y_{\mathrm L}=t+4,\quad z_{\mathrm L}=x+8.\] Mais le point $\mathrm L$ est aussi sur le plan $(\mathrm{IGJ})$, donc ses coordonnées en vérifient l'équation. \[\begin{aligned} &-x_{\mathrm L} + y_{\mathrm L} + z_{\mathrm L} - 4 = 0& \\ \iff &-(-t) + (t+4) + (t+8) - 4 = 0& \\ \iff &3t + 8 = 0& \\ \iff &t = -\frac83.& \end{aligned}\] Donc \[\begin{cases}x_{\mathrm L} = -\left(-\frac83\right) = \frac83\\ y_{\mathrm L}=-\frac83+4 = \frac43\\ z_{\mathrm L}=-\frac83+8=\frac{16}3 \end{cases} \implies L\left(\frac83;\frac43;\frac{16}3\right). \]

5. Calculer la distance du point $\mathrm H$ au plan $(\mathrm{IGJ})$.
Corrigé

Par définition, la distance du point $\mathrm H$ au plan $(\mathrm{IGJ})$ est $\mathrm{HL}$. \\ Or $\overrightarrow{\mathrm{HL}}$ a pour coordonnées \[ \begin{pmatrix}\frac83-0\\ \frac43-4\\ \frac{16}3-8\end{pmatrix} = \begin{pmatrix}\frac83\\-\frac83\\ -\frac83\end{pmatrix}.\] Donc: \[\mathrm{HL} = \sqrt{\left(\frac83\right)^2+\left(-\frac83\right)^2+\left(-\frac83\right)^2} =\frac{8\sqrt 3}3.\]

6. Montrer que le triangle $\mathrm{IGJ}$ est rectangle en $\mathrm I$.
Corrigé

On a déjà montré que $\overrightarrow{\mathrm{IJ}}\begin{pmatrix}-2\\0\\-2\end{pmatrix}$ et $\overrightarrow{\mathrm{IG}}\begin{pmatrix}2\\4\\-2\end{pmatrix}$.
Donc \[\overrightarrow{\mathrm{IJ}}\cdot\overrightarrow{\mathrm{IG}} =-2\times 2 + 0\times 4 + (-2)\times(-2) = 0.\] Puisque $\overrightarrow{\mathrm{IJ}}$ et $\overrightarrow{\mathrm{IG}}$ sont orthogonaux, le triangle $\mathrm{IJG}$ est rectangle en $\mathrm I$.

7. En déduire le volume du tétraèdre $\mathrm{IGJH}$.
Corrigé

Si l'on prend $\mathrm{IGJ}$ comme base du tétraèdre, alors la hauteur associée est $\mathrm{HL}$.
Donc le volume de ce tétraèdre est \[ \mathcal V = \frac{\mathrm{IG}\times\mathrm{IJ}}2 \times \mathrm{HL} \] Avec : \[\begin{aligned} \mathrm{IG} &= \sqrt{2^2+4^2+(-2)^2} = 2\sqrt 6\;;& \\ \mathrm{IJ} &= \sqrt{(-2)^2+0^2+(-2)^2} = 2\sqrt{2}.& \end{aligned}\] Donc : \[\mathcal V = \frac{2\sqrt{6}\times2\sqrt 2}{2}\times \frac{8\sqrt 3}3 = 16.\]

retour

code : 806