ex-289
retour
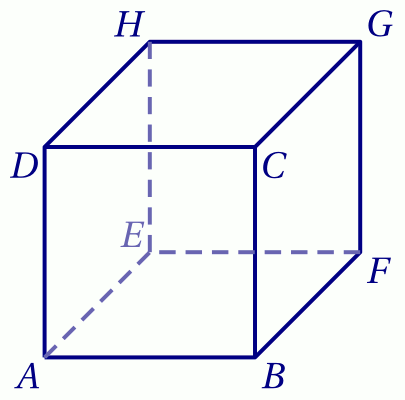
On considère le cube $ABCDEFGH$ ci-dessous.
1.
Montrer que
$\overrightarrow{AC}\cdot\overrightarrow{BE}= 0$
puis que
$\overrightarrow{AG}\cdot\overrightarrow{BD}=0$.
Indication
Corrigé
On pourra décomposer chaque vecteur selon les directions des arêtes du cube.
Après développement, on n'aura plus que des produits scalaires de vecteurs orthogonaux ou colinéaires.
Après développement, on n'aura plus que des produits scalaires de vecteurs orthogonaux ou colinéaires.
\[\begin{aligned}
\overrightarrow{AG}\cdot\overrightarrow{BE}
&=(\overrightarrow{AB}+\overrightarrow{BF}+\overrightarrow{FG})\cdot(\overrightarrow{BF}+\overrightarrow{FE})&
\\
&=\overrightarrow{AB}\cdot\overrightarrow{BF}
+ \overrightarrow{BF}\cdot\overrightarrow{BF}
+ \overrightarrow{FG}\cdot\overrightarrow{BF}&
\\
&\quad
+\overrightarrow{AB}\cdot\overrightarrow{FE}
+\overrightarrow{BF}\cdot\overrightarrow{FE}
+\overrightarrow{FG}\cdot\overrightarrow{FE}&
\\
&= 0 + BF^2 + 0 - AB^2 + 0 + 0&
\\
&=0.&
\end{aligned}\]
(car les arêtes $BF$ et $AB$ sont égales.)
De même : \[\begin{aligned} \overrightarrow{AG}\cdot\overrightarrow{BD} &=(\overrightarrow{AB}+\overrightarrow{BF}+\overrightarrow{GF}) \cdot(\overrightarrow{BA}+\overrightarrow{AD})& \\ &=\overrightarrow{AB}\cdot\overrightarrow{BA} + \overrightarrow{BF}\cdot\overrightarrow{BA} +\overrightarrow{FG}\cdot\overrightarrow{BA}& \\ &\quad + \overrightarrow{AB}\cdot\overrightarrow{AD} +\overrightarrow{BF}\cdot\overrightarrow{AD} + \overrightarrow{FG}\cdot\overrightarrow{AD}& \\ &= -AB^2 + 0 + 0 + 0 + 0 + AD^2& \\ &=0.& \end{aligned}\] (car $AB = AD$.)
De même : \[\begin{aligned} \overrightarrow{AG}\cdot\overrightarrow{BD} &=(\overrightarrow{AB}+\overrightarrow{BF}+\overrightarrow{GF}) \cdot(\overrightarrow{BA}+\overrightarrow{AD})& \\ &=\overrightarrow{AB}\cdot\overrightarrow{BA} + \overrightarrow{BF}\cdot\overrightarrow{BA} +\overrightarrow{FG}\cdot\overrightarrow{BA}& \\ &\quad + \overrightarrow{AB}\cdot\overrightarrow{AD} +\overrightarrow{BF}\cdot\overrightarrow{AD} + \overrightarrow{FG}\cdot\overrightarrow{AD}& \\ &= -AB^2 + 0 + 0 + 0 + 0 + AD^2& \\ &=0.& \end{aligned}\] (car $AB = AD$.)
2.
En déduire la position relative de la droite $(AG)$ et du plan $(BED)$.
Corrigé
$\overrightarrow{BE}$ et $\overrightarrow{BD}$, non colinéaires, forment une base du plan $(BED)$.
$\overrightarrow{AG}$, orthogonal à ces deux vecteurs, est donc normal au plan $(BED)$.
La droite $(AG)$ est donc perpendiculaire au plan $(BED)$.
$\overrightarrow{AG}$, orthogonal à ces deux vecteurs, est donc normal au plan $(BED)$.
La droite $(AG)$ est donc perpendiculaire au plan $(BED)$.
3.
En se plaçant dans le repère $\left(D;\overrightarrow{DA};\overrightarrow{DC};\overrightarrow{DH}\right)$,
déterminer les coordonnées des points $A$, $B$, $D$, $E$ et $G$ (aucune justification attendue).
Corrigé
$A(1;0;0)$, $B(1;1;0)$, $D(0;0;0)$, $E(1;0;1)$ et $G(0;1;1)$.
4.
Avec les coordonnées, démontrer que la droite $(AG)$ est orthogonale au plan $(BED)$.
Corrigé
On en déduit les coordonnées de :
Or : \[\begin{aligned} \overrightarrow{AG}\cdot\overrightarrow{BE} &= -1\times 0 + 1\times (-1) + 1\times 1 = 0\;;& \\ \overrightarrow{AG}\cdot\overrightarrow{ED} &= -1\times (-1) + 1\times 0 + 1\times (-1) = 0.& \end{aligned}\] $\overrightarrow{AG}$, orthogonal aux deux vecteurs d'une base de $(BED)$ est donc normal à $(BED)$. La droite $(AG)$ qu'il dirige est donc perpendiculaire à ce plan.
- $\overrightarrow{AG}$ : $\begin{pmatrix}0 - 1 \\ 1 - 0 \\ 1 - 0 \end{pmatrix} =\begin{pmatrix} -1 \\ 1 \\ 1\end{pmatrix}$.
- $\overrightarrow{BE}$: $\begin{pmatrix}1 - 1\\ 0 - 1\\1 - 0\end{pmatrix} =\begin{pmatrix}0 \\ -1 \\ 1\end{pmatrix}$.
- $\overrightarrow{ED}$: $\begin{pmatrix}0-1\\0-0\\0-1\end{pmatrix} =\begin{pmatrix}-1\\0\\-1\end{pmatrix}$.
Or : \[\begin{aligned} \overrightarrow{AG}\cdot\overrightarrow{BE} &= -1\times 0 + 1\times (-1) + 1\times 1 = 0\;;& \\ \overrightarrow{AG}\cdot\overrightarrow{ED} &= -1\times (-1) + 1\times 0 + 1\times (-1) = 0.& \end{aligned}\] $\overrightarrow{AG}$, orthogonal aux deux vecteurs d'une base de $(BED)$ est donc normal à $(BED)$. La droite $(AG)$ qu'il dirige est donc perpendiculaire à ce plan.
retour
code : 289