ex-409
retour
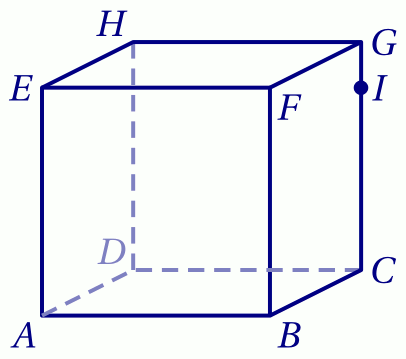
$ABCDEFGH$ est le cube ci-dessous, $I$ est un point de l'arête $[CG]$ distinct de $G$.
1.
Citer un vecteur normal au plan $(ABC)$.
Corrigé
$\overrightarrow{AE}$ (ou $\overrightarrow{BF}$, ou $\overrightarrow{CI}$ etc.)
2.
Le vecteur $\overrightarrow{EH}$ est-il un vecteur normal au plan $(GDC)$? Justifier.
Corrigé
$(\overrightarrow{HG},\overrightarrow{HD})$ est une base du plan $(GDC)$.
Or $\overrightarrow{EH}$ est orthogonal à la fois à $\overrightarrow{HG}$ et à $\overrightarrow{HD}$,
donc c'est bien un vecteur normal au plan $(GDC)$.
3.
Le vecteur $\overrightarrow{IF}$ est-il un vecteur normal au plan $(GCH)$? Justifier.
Corrigé
$\overrightarrow{IF}$ n'est pas orthogonal à $\overrightarrow{CG}$,
bien que les points $C$ et $G$ appartiennent au plan $(GCH)$.
Il n'est donc pas un vecteur normal au plan $(GCH)$.
Il n'est donc pas un vecteur normal au plan $(GCH)$.
4.
Le vecteur $\overrightarrow{BD}$ est-il un vecteur normal au plan $(GCA)$? Justifier.
Corrigé
$(\overrightarrow{AC},\overrightarrow{GC}=\overrightarrow{BF})$ est une base du plan $(GCA)$.
Or $\overrightarrow{BD}$ est orthogonal à la fois à $\overrightarrow{AC}$ et à $\overrightarrow{BF}$.
Donc $\overrightarrow{BD}$ est bien un vecteur normal au plan $(GCA)$.
Donc $\overrightarrow{BD}$ est bien un vecteur normal au plan $(GCA)$.
retour
code : 409