retour

ABCDEFGH est un parallélépipède rectangle tel que $\mathrm{AE}=\mathrm{AD}=a$ et $\mathrm{AB} = 3a$ ($a\in\mathbb R_+^*$).

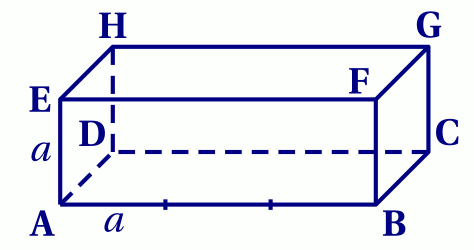
Exprimer en fonction de $a$ les produits scalaires suivants (expliciter la méthode utilisée):

1. $\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AF}}$;     Corrigé
   $F$ se projette orthogonalement sur $(AB)$ en $B$ donc: \[\overrightarrow{AB}\cdot\overrightarrow{AF} =AB\times AB = (3a)^2 = 9a^2.\]
2. $\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AG}}$;     Corrigé
   $G$ se projette orthogonalement sur $(AB)$ en $B$ donc: \[\overrightarrow{AB}\cdot\overrightarrow{AG} =AB^2 = 9a^2.\]
3. $\overrightarrow{\mathrm{EG}}\cdot\overrightarrow{\mathrm{HF}}$;     Corrigé
   Décomposons selon les directions des arêtes: \[\begin{aligned} \overrightarrow{EG}\cdot\overrightarrow{HF} &=\left(\overrightarrow{EF}+\overrightarrow{FG}\right)\cdot \left(\overrightarrow{HG}+\overrightarrow{GF}\right)& \\ &={\small \underbrace{\overrightarrow{EF}\cdot\overrightarrow{HG}}_{EF\times HG} +\underbrace{\overrightarrow{EF}\cdot\overrightarrow{GF}}_0 +\underbrace{\overrightarrow{FG}\cdot\overrightarrow{HG}}_0 +\underbrace{\overrightarrow{FG}\cdot\overrightarrow{GF}}_{-FG^2}}& \\ &=9a^2 - a^2 = 8a^2.& \end{aligned}\]
4. $\overrightarrow{\mathrm{AH}}\cdot\overrightarrow{\mathrm{DB}}$.     Corrigé
   Décomposons à nouveau : \[\begin{aligned} \overrightarrow{AH}\cdot\overrightarrow{DB} &=\left(\overrightarrow{AD}+\overrightarrow{DH}\right)\cdot \left(\overrightarrow{DC}+\overrightarrow{CB}\right)& \\ &={\small\underbrace{\overrightarrow{AD}\cdot\overrightarrow{DC}}_0 +\underbrace{\overrightarrow{AD}\cdot\overrightarrow{CB}}_{-AD^2} +\underbrace{\overrightarrow{DH}\cdot\overrightarrow{DC}}_0 +\underbrace{\overrightarrow{DH}\cdot\overrightarrow{CB}}_0}& \\ &=-a^2.& \end{aligned}\]
Corrigé par une méthode alternative
On peut se placer dans une base orthonormée, par exemple \[\left(\frac 1 3\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AE}\right).\] Alors :
1. $\overrightarrow{AB}(3a;0;0)$ et $\overrightarrow{AF}(3a;0;a)$ donc \[\overrightarrow{AB}\cdot\overrightarrow{AF} = (3a)^2 + 0^2 + 0\times a = 9a^2.\]
2. $\overrightarrow{AB}(3a;0;0)$ et $\overrightarrow{AG}(3a;a;a)$ donc \[\overrightarrow{AB}\cdot\overrightarrow{AG} = (3a)^2 + 0\times a + 0\times a = 9a^2.\]
3. $\overrightarrow{EG}(3a;a;0)$ et $\overrightarrow{HF}(3a;-a;0)$ donc \[\overrightarrow{EG}\cdot\overrightarrow{HF} =(3a)^2 + a\times (-a) + 0\times 0 = 8a^2.\]
4. $\overrightarrow{AH}(0;a;a)$ et $\overrightarrow{DB}(3a;-a;0)$ donc \[\overrightarrow{AH}\cdot\overrightarrow{DB} =0\times 3a + a \times (-a) + a \times 0 = -a^2.\]

retour

code : 630