Probabilités
Cours

retour

1. Langage des événements

1.1. Expérience aléatoire

Une expérience aléatoire est une expérience dont le résultat est lié uniquement au hasard et ne peut donc pas être connu à l’avance.

Tout résultat possible de l’expérience s’appelle une issue.

L’ensemble des issues s’appelle univers de l’expérience. On le note souvent Ω.

Exemple (fil rouge)

Soit ℰ l’expérience « on jette un dé et on note le numéro obtenu ».
Une issue possible est 3.
L’univers de ℰ est Ω={1;2;3;4;5;6}.

1.2. Événements

Déf. Un événement est un ensemble d’issues. On le note avec une lettre majuscule.
On dit que cet événement est réalisé si le résultat de l’expérience appartient à l’événement.

Ex. (fil rouge suite) Dans ℰ l’événement A « tirer un numéro impair » est A = {1;3;5}. L’événement B « tirer un nombre supérieur ou égal à 3 » est B = {3;4;5;6}.
Si l’on sort un 1 avec le dé, alors A est réalisé car 1∈A mais B ne l’est pas car 1∉B.

On peut représenter des événements à l’aide d’un diagramme de Venn comme ci-dessous.

Ex. (fil rouge, suite)

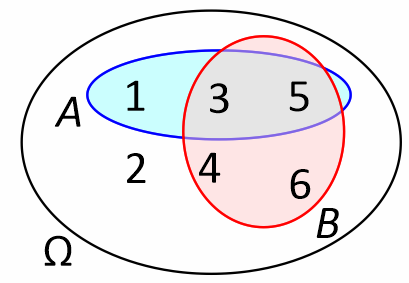
Rem. L’univers Ω est lui-même un événement : il représente l’événement certain.

Déf. Il existe un événement spécial qui ne contient aucune issue. On l'appelle événement impossible (ou événement vide). On le note ∅.

1.3. Opérations sur les événements

Soient $A$ et $B$ deux événements d’une expérience aléatoire donnée.

Déf.

L’événement formé de toutes les issues qui se trouvent dans $A$ ou dans $B$ s’appelle l’union de $A$ et $B$ et se note $A\cup B$.
L’événement formé des issues qui sont à la fois dans $A$ et dans $B$ s’appelle intersection de $A$ et $B$ et se note $A\cap B$.
L’événement formé de toutes les issues qui ne sont pas dans $A$ s’appelle contraire de $A$ et se note $\overline A$.

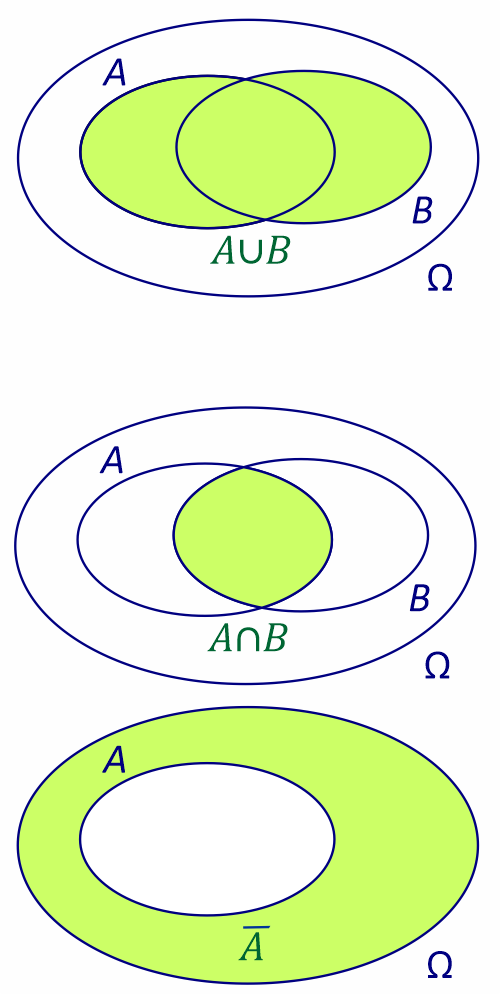
Illustration avec des diagrammes de Venn

Ex. (fil rouge, suite)

$A\cup B = \{1\;;\;3\;;\;4\;;\;5\;;\;6\}$.
$A\cap B = \{3\;;\;5\}$.
$\overline A = \{2\;;\;4\;;\;6\}$.
$\overline B = \{1\;;\;2\}$.

Déf. Deux événements A et B sont dits incompatibles s'ils ne peuvent pas être réalisés en même temps, donc si A∩B = ∅.

Exercices
EX-01 EX-02 EX-03

2. Probabilité d’un événement

2.1. Probabilité et fréquence

La probabilité d’un événement est un nombre qui évalue « nos chances » d’obtenir cet événement.

On peut donc l’estimer en répétant un très grand nombre de fois cette expérience, et en calculant la fréquence de réalisation de l’événement.
On calcule donc :

La probabilité est le nombre que l'on obtiendrait en répétant infiniement cette expérience.

Déf. Soit $\Omega=\{e_1,e_2,\ldots,e_n\}$ l’univers de l’expérience aléatoire.
On définit une loi de probabilité sur $\Omega$ en attribuant à chaque issue $e_i$ (avec $1\le i \le n$) un nombre réel de l’intervalle $[0;1]$, appelé probabilité de $e_i$ et notée $P(e_i)$ tel que : \[P(e_1)+P(e_2)+\cdots+P(e_n)=1.\] La probabilité de tout événement $A$ est alors définie comme la somme des probabilités des issues qui le composent . \[A=\{e_1,\cdots,e_k\}\implies P(A)=P(e_1)+\cdots+P(e_k).\]

Exemple.

On dispose d’un dé pipé (truqué). Les probabilités d’obtenir chaque face sont données dans le tableau ci-dessous.

face	1	2	3	4	5	6
probabilité	0,15	0,20	0,10	0,17	0,13	?

La probabilité d’obtenir 3 est $P(3)=0,10$.
Soit $A$ l’événement « le nombre obtenu est au plus égal à 3 ». \[A = \{1,2,3\}\] Donc \[P(A)= 0,15+0,20+0,10 =0,45.\] La somme de toutes les probabilités doit être égale à 1, donc La probabilité d’obtenir 6 est : \[P(6)=1-0,15-0,2-0,1-0,17-0,13=0,25.\]

2.2. Équiprobabilité

Déf. On dit qu'on est en situation d'équiprobabilité si toutes les issues ont la même probabilité.

Prop. Soit une expérience aléatoire en situation d'équiprobabilité dont l'univers comporte $n$ issues.
Chaque issue a pour probabilité $\dfrac 1 n$.
Si un événement comporte $k$ issues, sa probabilité est $\dfrac k n$.

2.3. Probabilité d’une union

Prop. Soient $A$ et $B$ deux événements. Alors \[P(A\cup B)=P(A)+P(B)-P(A\cap B).\]

Preuve. Pour calculer $P(A)+P(B)$, on additionne les probabilités des issues situées dans $A$ et des issues situées dans $B$.
Ce faisant, on a compté deux fois les probabilités des issues situées à la fois dans $A$ et dans $B$, qu'il faut donc enlever une fois.

Coro. Si $A$ et $B$ sont deux événements incompatibles (donc $A\cap B=\emptyset$) : \[P(A\cup B)=P(A)+P(B).\]

Preuve.

\[\begin{aligned} P(A\cup B) &= P(A) + P(B) - P(A\cap B)& \\ &=P(A) + P(B) - P(\emptyset)& \\ &=P(A) + P(B) + 0.& \end{aligned}\]

Coro. Pour tout événement $A$ : $P(\overline A) = 1 - P(A)$.

Preuve.

Sachant que $A$ et $\overline A$ sont incompatibles: \[\begin{aligned} P(A) + P(\overline A) &= P(A\cup \overline A)& \\ \iff P(A) + P(\overline A) &= P(\Omega)& \\ \iff P(A) + P(\overline A) &=1& \\ \iff P(\overline A) &= 1 - P(A).& \end{aligned}\]

Exercices corrigés.
EX-04 EX-05 EX-06 EX-07 EX-08 EX-09 EX-10 EX-11 EX-12 EX-13 EX-14 EX-15 EX-16

3. Techniques de dénombrement (exemples)

En probabilités, on est souvent amené à devoir dénombrer des issues. Nous rappelons en exemple deux méthodes de dénombrement classiques.

3.1. Tableau

Expérience : On jette simultanément deux dés équilibrés à six faces et on note la somme des points obtenus.
On cherche la probabilité de l’événement $A$ : « obtenir une somme égale à 5 ».
On peut modéliser cette expérience par le tableau à double entrée ci-dessous.

1^er dé↓ 2^e dé→	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

Le tableau dénombre 36 issues équiprobables. On compte 4 issues donnant une somme égale à 5. Donc : \[P(A)=\frac{4}{36} = \frac 1 9.\]

3.2. Arbre de dénombrement

On jette trois fois de suite une pièce équilibré, en notant à chaque fois si elle tombe sur « pile » ou « face ».
$B$ est l’événement « obtenir au moins deux fois "pile" ».

On peut modéliser ces trois lancers par l’arbre ci-dessous.

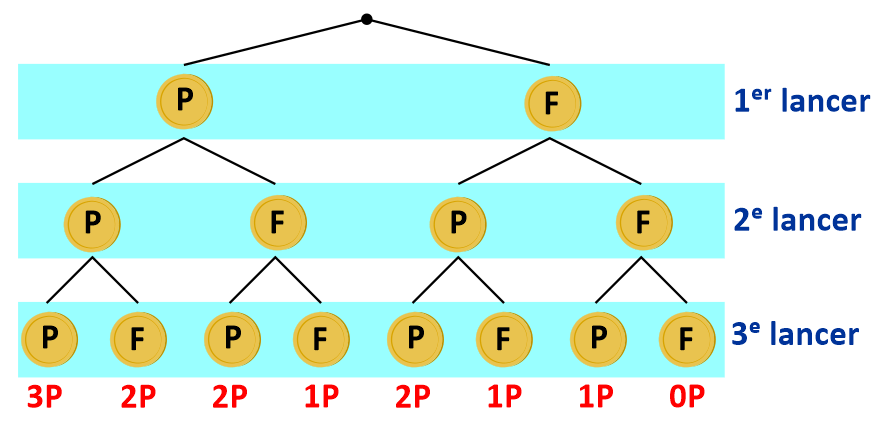
Il permet de lister toutes les issues possibles (de gauche à droite) :
PPP, PPF, PFP, PFF, FPP, FPF, FFP et FFF.
Parmi ces 8 issues, 4 correspondent à deux ou trois piles obtenus. Donc \[P(B) = \frac 4 8 = \frac 1 2.\]

Exercices corrigés
EX-17 EX-18 EX-19 EX-20 EX-21 EX-22 EX-23 EX-24