retour

Jules et Paul jouent aux dés. Ces dés sont équilibrés.

1. Est-ce que, lors du jet d'un dé, la probabilité d'obtenir un est la même que celle d'obtenir un  ? Expliquer.
   Corrigé
   Les probabilités d'obtenir "1" ou "5" sont les mêmes car, d'après la consigne, le dé est équilibré donc chaque face a autant de chances d'être obtenue qu'une autre.
   On dit qu'il y a équiprobabilité des issues.
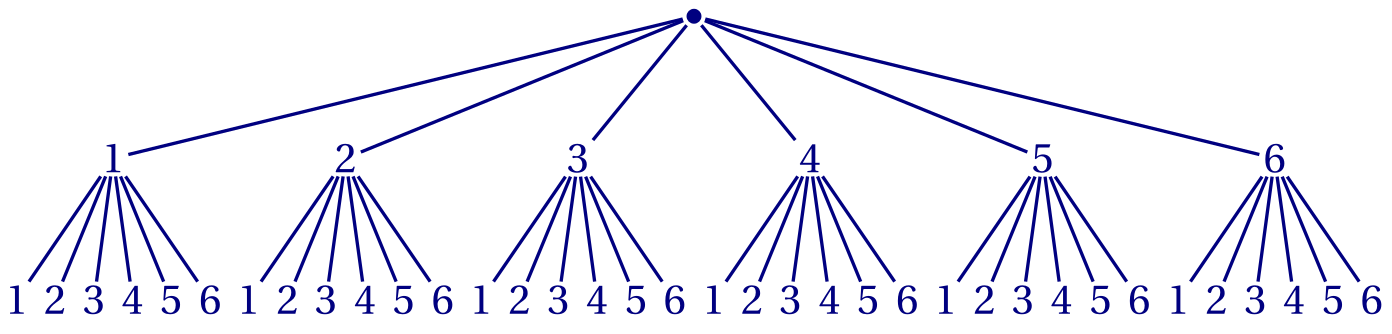
2. Jules lance en même temps un dé rouge et un dé jaune. Par exemple il peut obtenir 3 au dé rouge et 4 au dé jaune, c'est l'une des issues possibles. Expliquer pourquoi le nombre d'issues possibles quand il lance ses deux dés est de 36.
   Corrigé
   Il y a 6 résultats possibles pour le dé rouge. On peut associer à chacun de ces résultats 6 résultats possibles pour le dé jaune. Il y a donc en tout
   6×6 = 36 issues possibles.
   
3. Jules propose à Paul de jouer avec ces deux dés (un jaune et un rouge), Il lui explique la règle :
   • Le gagnant est le premier à remporter un total de 1000 points.
   • Si, lors d'un lancer, un joueur fait , c'est-à-dire une paire de "1", il remporte 1000 points (et donc la partie).
   • Si un joueur obtient une paire de 2, il obtient 100 fois la valeur du 2, soit 2×100 = 200 points.
   • De même, si un joueur obtient une paire de 3 ou de 4 ou de 5 ou 6, il obtient 100 fois la valeur du dé.
   • Si un joueur obtient un résultat autre qu'une paire (exemple sur le dé jaune et sur le dé rouge), il obtient 50 points.
   
   Paul a déjà fait 2 lancers et a obtenu 650 points.
   Quelle est la probabilité qu'il gagne la partie à son troisième lancer ?
   Corrigé
   Paul doit réaliser au moins 1000 − 650 = 350 points lors de son prochain lancer.
   Il lui faut donc réaliser soit un double 1, soit un double 4, soit un double 5, soit un double 6.
   La probabilité d'y parvenir est donc : \[\frac{4}{36} = \frac 1 9.\]

retour

code : 144