retour

Une urne contient quatre boules numérotées de 1 à 4. On tire au hasard une première boule de l'urne puis, sans la remettre, on tire une seconde boule.

Dans la suite, on note $(a,b)$ l'issue «la première boule porte le numéro $a$ puis la seconde porte le numéro $b$».

1. Déterminer l'univers de cette expérience aléatoire ; On pourra s'aider d'un arbre.
   Corrigé
   Il y a $4\times 3 = 12$ tirages possibles et l'univers est \[{\scriptsize \Omega = \big\{(1,2);(1,3);(1,4);(2,1);(2,3),(2,4);(3,1);(3,2);(3,4);(4,1);(4,2);(4,3)\big\}}\] On pouvait réaliser l'arbre suivant.
   
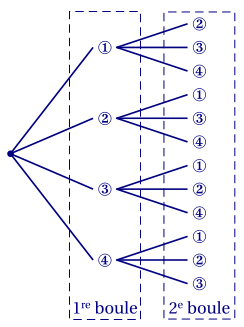
2. Écrire
   en extensionen donnant toutes les issues qui le composent
   les événements
   • $A$ : «le numéro tiré en premier est 2» ;
     Corrigé
     \[ A =\big\{(2,1),\ (2,3),\ (2,4)\big\}.\]
   • $B$ : «la somme des deux numéros tirés est 5».
     Corrigé
     \[B =\big\{(1,4),\ (2,3),\ (3,2),\ (4,1)\big\}.\]
3. Écrire
   en extensionen donnant toutes les issues qui le composent
   l'événement $A\cap B$.
   Corrigé
   \[A\cap B = \big\{(2;3)\big\}.\]
4. Indiquer la probabilité de chacun des événements
   • $A$, Corrigé
     \[P(A) = \frac{3}{12} = \frac 1 4.\]
   • $B$, Corrigé
     \[P(B) = \frac 4 {12} = \frac 1 3.\]
   • $A\cap B$. Corrigé
     \[P(A\cap B) =\frac 1 {12}.\]
5. Déterminer de deux façons différentes la probabilité de l'événement $A\cup B$.
   Méthode 1   Méthode 2
   \[A\cup B = \{(1,4),\ (2,1),\ (2,3),\ (2,4),\ (3,2),\ (4,1)\}.\] Donc \[P(A\cup B) = \dfrac{6}{12}=\dfrac 1 2.\]
   \[\begin{aligned} P(A\cup B) &= P(A) + P(B) - P(A\cap B)&\\ &=\dfrac{3}{12}+\dfrac{4}{12} -\dfrac 1 {12}& \\ &= \dfrac{6}{12}=\dfrac 1 2.& \end{aligned}\]

retour

code : 153