0. Révisions

Dérivation d'une fonction

1. Définition

Théo. & Déf. On admet l'existence et l'unicité d'une fonction appelée fonction exponentielle, notée $x\mapsto \exp(x)$ ou $x\mapsto \mathrm e^x$ telle que&:

La fonction exponentielle est dérivable sur $\mathbb R$ et elle est sa propre fonction dérivée;
$\mathrm \exp(0)= \mathrm e^0 = 1$.

Déf. On note $\mathrm e = \exp(1)=\mathrm e^1$. $\mathrm e$ est un nombre irrationnel dont la valeur est voisine de 2,718.

2. Courbe de la fonction exponentielle

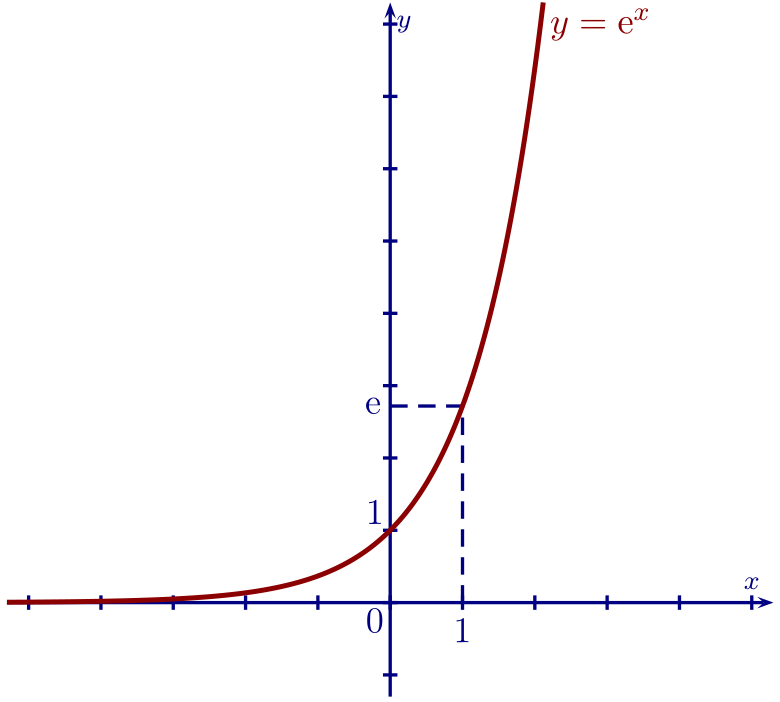
2. Dérivation d'une composée

Prop. Soit $u$ une fonction dérivable sur un ensemble $D$. Alors la fonction \[x\mapsto \mathrm e^{u(x)}\] est aussi dérivable sur $D$, de fonction dérivée \[x\mapsto u'(x)\mathrm e^{u(x)}.\]

3. Étude de la fonction exponentielle

Prop. Pour tout réel $x$, $\mathrm e^x > 0$.

Donc la fonction exponentielle a une dérivée strictement positive, ce qui justifie la propriété suivante.

Prop. La fonction exponentielle est strictement croissante sur $\mathbb R$.

On en déduit les équivalences suivantes.

Prop. \[\begin{aligned} \forall a\in\mathbb R,\forall b\in\mathbb R,\quad &\mathrm e^a = \mathrm e^b \iff a = b& \\ &\mathrm e^a < \mathrm e^b \iff a < b.& \\ &\mathrm e^a \leqslant \mathrm e^b \iff a \leqslant b.& \\ &\mathrm e^a > \mathrm e^b \iff a > b.& \\ &\mathrm e^a \geqslant \mathrm e^b \iff a \geqslant b.& \end{aligned}\]

Exercices
EX-01 EX-02 EX-03

4. Propriétés algébriques de l'exponentielle

Rem. Le symbole $\forall$ utilisé ci-après se lit « quel que soit » (ou encore « pour tout »).

Prop. \[\forall a\in\mathbb R,\ \forall b\in\mathbb R,\quad \mathrm e^{a+b} =\mathrm e^{a}\cdot\mathrm e^{b}\]

Prop. \[\forall a\in\mathbb R,\ \mathrm e^{-a} = \frac 1 {\mathrm e^a}.\]

Prop. \[\forall a\in\mathbb R,\forall b\in\mathbb R,\quad \mathrm e^{a-b} = \frac{\mathrm e^a}{\mathrm e^b}.\]

Prop. \[\forall a\in\mathbb R,\forall n\in\mathbb Z,\quad \left(\mathrm e^a\right)^n = \mathrm e^{na}.\]

Exercices

Travailler des expressions avec exponentielle.
EX-04 EX-05 EX-06 EX-07 EX-08 EX-09

Résoudre des équations, inéquations, systèmes.
EX-10 EX-11 EX-12 EX-13 EX-14