0 - Révisions

Fonctions affines

Droites

1. Nombre dérivé

Dans toute cette section, on considère une fonction $f$, définie sur un intervalle $I$ fermé.
$\mathscr C$ est la représentation graphique de $f$ dans un repère quelconque.

1.1. Sécante et taux de variation

Déf. Soient $a\in I$ et $b\in I$ distincts. On appelle taux de variation entre $a$ et $b$ le nombre réel : \[\frac{f(b)-f(a)}{b-a}.\]

Rem. Si $A$ et $B$ sont les points de $\mathscr C$ d'abscisses respectives $a$ et $b$, le taux de variation entre $a$ et $b$ est aussi le coefficient directeur de la droite $(AB)$.

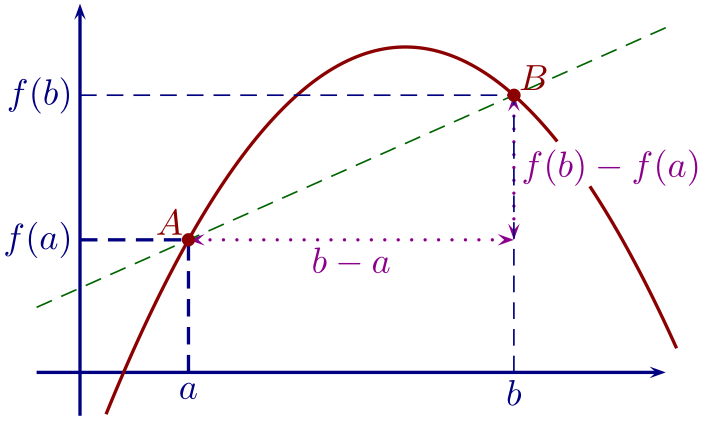
Rem. Si l'on appelle $h$ l'écart entre $a$ et $b$ : $h = b - a$, alors le taux de variation s'écrit aussi : \[\frac{f(b)-f(a)}{b-a} = \frac{f(a+h) - f(a)}{h}.\]

1.2. Construction du nombre dérivé

Déf. Soit $f$ une fonction définie sur un intervalle fermé $I$, et $a\in I$.
Si, plus le réel $h$ se rapproche de $0$, plus le quotient \[\frac{f(a+h) - f(a)}h\] se rapproche d'un certain nombre réel $\ell$, on dira que ce rapport a pour limite $\ell$ quand $h$ tend vers $0$.
On le note : \[\lim_{h\to 0} \frac{f(a+h) - f(a)}h = \ell\]

Déf. S'il existe un réel $\ell$ tel que \[\lim_{h\to 0} \frac{f(a+h) - f(a)}h = \ell\] alors on dit que $f$ est dérivable en $a$. $\ell$ s'appelle le nombre dérivé de $f$ en $a$. On le note $\ell=f'(a)$.

Ex. Soit par exemple la fonction $f: x\mapsto x^2$ et $a$ un réel quelconque. Alors : \[\begin{aligned} \frac{f(a+h) -f(a)}{h} &= \frac{(a+h)^2 - a^2}{h}& \\ &=\frac{a^2 + 2ah + h^2 - a^2}{h}& \\ &= \frac{2ah +h^2}{h} = \frac{h(2a+h)}{h}& \\ &=2a+h.& \end{aligned}\] On en déduit que \[\lim_{h\to 0} \frac{f(a+h) - f(a)}h = \lim_{h\to 0} 2a+h = 2a\] La fonction $x\mapsto x^2$ est donc dérivable en tout réel $a$.
De plus, le nombre dérivé en $a$ est $2a$, ce qui s'écrit aussi \[f'(a) = 2a.\]

Exercices

EX-01

Tangente

Rem. Graphiquement, faire tendre $h$ vers $0$ revient à rapprocher de plus en plus le point $B$ du point $A$.
S'il existe un réel $\ell$ tel que \[\lim_{h\to 0} \frac{f(a+h) - f(a)}h = \ell,\] alors ce réel est le coefficient directeur de la droite que l'on obtient au moment ou le point $B$ rejoint le point $A$.
Cette droite s'appelle la tangente à $\mathscr C$ en $a$.

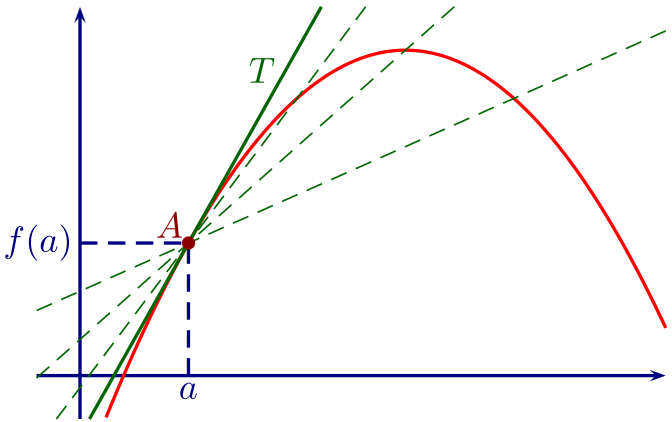
Déf. Si $f$ est dérivable en $a$, on appelle tangente en $a$ à $\mathscr C$ la droite de coefficient directeur $f'(a)$ qui passe par le point d'abscisse $a$ de $\mathscr C$.

Prop. Si $f$ est dérivable en $a$, alors la tangente en $a$ à sa courbe admet pour équation \[y = f'(a)(x-a) + f(a).\]

Démo.

Puisque $f'(a)$ est le coefficient de cette droite, elle admet une équation affine de la forme \[y = mx + p\] où $m = f'(a)$ et où l'ordonnée à l'origine $p$ reste à déterminer.
On sait de plus que $A(a;f(a))$ appartient à cette droite, donc \[\begin{aligned} y_A &= mx_A + p& \\ \iff f(a) &= f'(a)a + p& \\ \iff p &= f(a) - f'(a)a.& \end{aligned}\] L'équation de la tangente est donc \[\begin{aligned} y &= mx + p& \\ \iff y &= f'(a)x + f(a) -f'(a)a& \\ \iff y &= f'(a)(x-a) + f(a).& \end{aligned}\]

Exercices

EX-02

3. Fonction dérivée

Déf. Si, pour tout réel $a$ d'un intervalle $J\subset I$, $f$ est dérivable en $a$, alors on dit que la fonction $f$ est dérivable sur $J$, et la fonction $a\mapsto f'(a)$ est appelée fonction dérivée de $f$.

Ex. On a déjà montré dans un exemple précédent que la fonction $x\mapsto x^2$ est dérivable sur $\mathbb R$ et que sa fonction dérivée est $x\mapsto 2x$.

Ex. Considérons maintenant la fonction $x\mapsto \dfrac 1 x$. Pour tout réel $a\neq 0$ : \begin{align*} \frac{f(a+h) - f(a)}{h} &= \frac{\frac{1}{a+h} - \frac 1 a}{h}& \\ &=\frac{\frac{a-(a+h)}{a(a+h)}}h& \\ &=\frac{a-a-h}{a(a+h)} \times \frac 1 h& \\ &=-\frac{h}{a(a+h)}\times \frac 1 h& \\ &=-\frac1{a(a+h)}.& \end{align*} Donc : \[\begin{aligned} &\lim_{h\to 0} \frac{f(a+h) -f(a)}{h}& \\ =&\lim_{h\to0} -\frac 1 {a(a+h)}& \\ =&-\frac 1 {a\times (a+0)}& \\ =&-\frac 1 {a^2}.& \end{aligned}\] Ceci prouve que la fonction $x\mapsto \dfrac 1 x$ est dérivable sur $]-\infty;0[\cup]0;+\infty[$ et que sa fonction dérivée est $x\mapsto -\dfrac 1 {x^2}$.

4. Calcul de fonction dérivées

4.1. Fonctions dérivées classiques

En procédant plus ou moins comme dans les exemples précédents, on a déterminé l'ensemble de dérivation et la fonction dérivée de quelques fonctions de référence. Le tableau ci-après résume ces résultats. \[\begin{array}{|c|c|c|c|} \hline f(x) = & \text{définie sur} & \text{dérivable sur}&f'(x)= \\ \hline a,\quad a\in\mathbb R & \mathbb R & \mathbb R & 0 \\ \hline ax,\quad a\in\mathbb R & \mathbb R & \mathbb R & a \\ \hline \rule[0pt]{0mm}{1em}x^2 & \mathbb R & \mathbb R & 2x \\ \hline \rule{0mm}{1.1em}x^n,\quad n\in\mathbb N & \mathbb R & \mathbb R & nx^{n-1} \\ \hline \rule[-6pt]{0pt}{1.8em}\dfrac 1 x & \mathbb R^* & \mathbb R^* & -\dfrac 1 {x^2} \\ \hline \rule[0pt]{0pt}{1.1em}x^n,\quad n\in\mathbb Z^*_-&\mathbb R^* & \mathbb R^* & nx^{n-1} \\ \hline \rule[-7.5pt]{0pt}{1.9em}\sqrt{x} & \mathbb R_+ & \mathbb R_+^* & \dfrac 1 {2\sqrt x} \\ \hline \end{array} \]

4.2. Opérations sur les fonctions dérivées

À partir des dérivées données dans le tableau, on peut calculer d'autres fonctions dérivées en utilisant les propriétés admises suivantes.

Prop. (linéarité.) Soient $u$ et $v$ deux fonctions dérivables sur un même ensemble $I$ et $k$ un réel quelconque.
Alors :

$ku$ est dérivable sur $I$ et $\left(ku\right)'=ku'$.
$u+v$ est dérivable sur $I$ et $\left(u+v\right)'=u'+v'$.

Prop. Soient $u$ et $v$ deux fonctions dérivables sur un même ensemble $I$. Alors :

$uv$ est aussi dérivable sur $I$ et $\left(uv\right)' = u'v + uv'$.
Si $v$ ne s'annule pas sur $I$, alors $\dfrac u v$ est dérivable sur $I$ et : \[\left(\frac u v\right)' = \frac{u'v - uv'}{v^2}.\]
On en déduit que si $u$ ne s'annule pas sur $I$, alors $\dfrac 1 u$ est dérivable sur $I$ et : \[\left(\frac 1 u\right)' = -\frac{u'}{u^2}.\]

Prop. (composition.) Soit $u$ une fonction dérivable sur un ensemble $D$, dont les images sont dans un ensemble $E$.
Soit $f$ une fonction dérivable sur $E$.
Alors la fonction définie sur $D$ par \[x\mapsto f\left(u(x)\right)\] est dérivable sur $D$ sa fonction dérivée est : \[x\mapsto u'(x)f'\left(u(x)\right).\]

Exercices

EX-03 EX-04 EX-05 EX-06 EX-07 EX-08 EX-09

5. Application aux variations d'une fonction

Si $f$ est dérivable en $a$, alors au « voisinage » de $a$, la courbe $\mathscr C$ et la tangente en $a$ "collent" l'une à l'autre et ont donc la même variation.
Nous serons donc conduits à admettre le résultat essentiel suivant.

Théo. Si $f$ est dérivable sur un intervalle $I$ et que pour tout $x\in I$ :

$f'(x)\geqslant 0$, alors la fonction $f$ est croissante sur $I$ ;
$f'(x) = 0$, alors la fonction $f$ est constante sur $I$ ;
$f'(x) \leqslant 0$, alors la fonction $f$ est décroissante sur $I$.

Exercices

EX-10 EX-11 EX-12