1. Fonction affine.

Déf. Une fonction $f$ est dite affine s’il existe deux réels $m$ et $p$ tels que, pour tout $x\in\mathbb R$: \[f(x)=mx+p.\]

Voc. Le réel $m$ s’appelle le coefficient directeur tandis que le réel $p$ s’appelle l’ordonnée à l’origine.

Déf. Si $p=0$, donc si $f(x)=mx$, la fonction $f$ est non seulement affine mais aussi linéaire.
Les fonctions linéaires traduisent des situations de proportionnalité.

Prop. La représentation graphique d’une fonction est une droite si et seulement si cette fonction est affine.
Cette droite passe par le point de coordonnées $(0;p)$.

Prop. Une fonction affine est aussi linéaire si et seulement si sa représentation graphique passe par l’origine du repère.

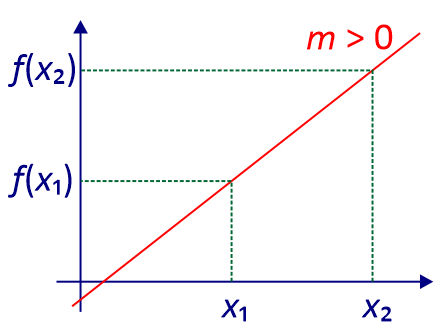
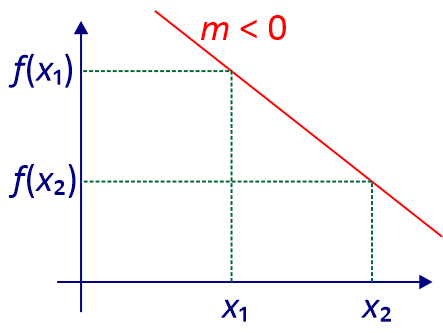
Prop. Soient $f:x\mapsto mx+p$ une fonction affine, $x_1$ et $x_2$ deux réels distincts.
Alors le coefficient directeur de f est : \[m=\frac{f(x_2 )-f(x_1 )}{x_2-x_1}.\]

2. Variation d’une fonction affine

Déf. Soit $I$ un intervalle. Si pour tous réels $x_1$ et $x_2$ de $I$, \[x_1<x_2 \implies f(x_1)\le f(x_2)\] on dit que la fonction $f$ est croissante sur $I$.
Si pour tous réels $x_1$ et $x_2$ de $I$, \[ x_1<x_2 \implies f(x_1)\ge f(x_2)\] la fonction f est décroissante sur $I$.
S'il existe un réel $k$ tel que, pour tout $x$ de $I$, $f(x)=k$, on dit que $f$ est constante sur $I$.

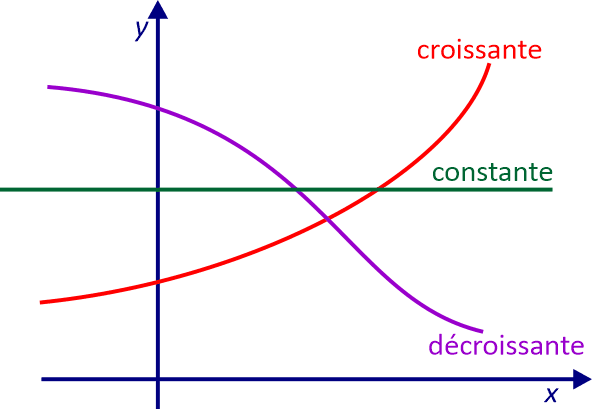
Prop. Soit $f:x\mapsto mx+p$ une fonction affine.

$f$ est croissante sur $\mathbb R$ si et seulement si $m\ge 0$;
$f$ est décroissante sur $\mathbb R$ si et seulement si $m\le 0$;
$f$ est constante si et seulement si $m=0$.

On a donc les tableaux de variation suivants :

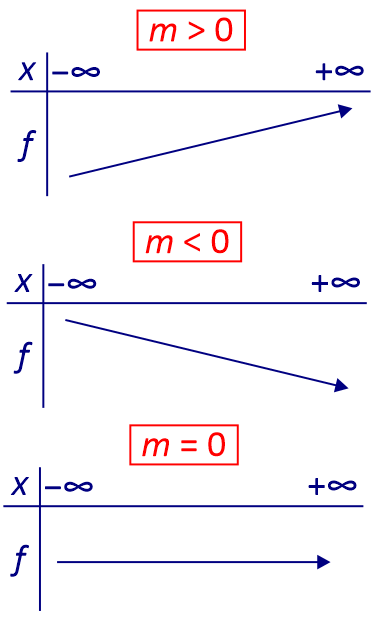
3. Signe d’une fonction affine

Dans cette section, on considère une fonction affine \[f:x\mapsto mx+p\] non constante (donc telle que $m\neq 0$).

Prop. & déf. On appelle "zéro" ou racine de $f$ l'unique réel $x_0$ tel que \[f(x_0)=0.\]

Rem. \[x_0 =- \frac{p}{m}.\]

Prop.

Si $m>0$, la fonction $f$ est croissante et donc \[f(x)>0 \iff x>x_0.\]
Si $m<0$, la fonction $f$ est décroissante et donc \[f(x)>0 \iff x<x_0.\]

On résume cette information par la phrase « une fonction affine est toujours du signe de son coefficient directeur à droite de son zéro ».

En pratique, on obtient donc les tableaux de signes suivants.

4. Signe d’un produit ou quotient de fonctions affines

On utilise la règle des signes : le produit (ou quotient) de deux fonctions dont on connaît les signes peut être obtenu à partir des signes de ces fonctions.
On utilise un tableau pour synthétiser l'étude.

Ex. Étudier le signe de \[x\mapsto \frac{2x-5}{3-x}.\] Le numérateur $x\mapsto 2x+5$ est une fonction affine s’annulant quand: \[2x-5=0\iff 2x=5 \iff x=\frac 5 2.\] Le dénominateur est une fonction affine s’annulant en 3.
Le coefficient directeur du numérateur, 2, est positif, donc le numérateur est positif à droite de $\frac 52$.
Le coefficient directeur du dénominateur est $-1$, négatif, donc il est positif à gauche de $3$.
On en déduit le tableau suivant.

Avec ce tableau, on peut, par exemple, résoudre :

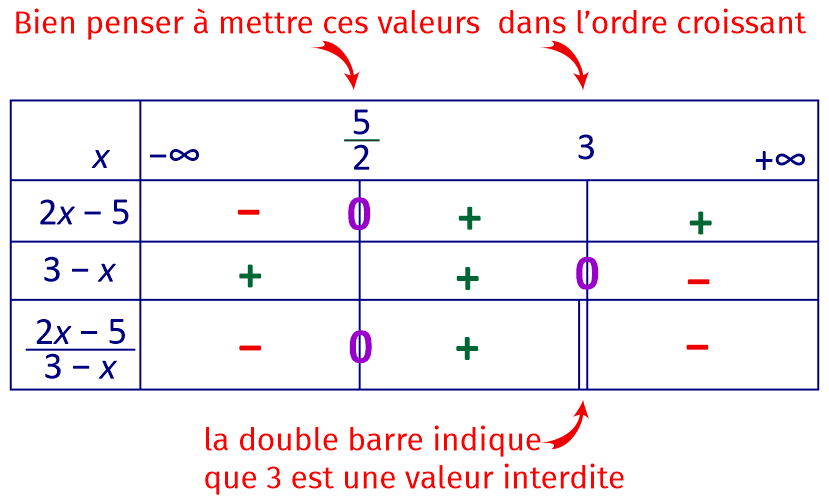
l’inéquation $\dfrac{2x-5}{3-x}\ge0$ qui a pour ensemble solution $S=\left[\dfrac 5 2\;;\;3\right[$.
l’inéquation $\dfrac{2x-5}{3-x}<0$ qui a pour ensemble solution $S = \left]-\infty;\dfrac 5 2\right[\cup\left]3;+\infty\right[$.