N. Belliard
Compléments des cours
T.MATHSGR1
X. Intégrales

retour

Sommaire

Corrigés d'exercices du manuel
Exercices supplémentaires en ligne (corrigés)
Démonstration de cours

Corrigés d'exercices du manuel

57 p. 382 59 p. 382 61 p. 382 76 p. 384 77 p. 384 78 p. 384 79 p. 384 80 p. 384 81 p. 384 89 p. 385 90 p. 385 91 p. 385 103 p. 386 104 p. 386 114 p. 387 116 p. 387 124 p. 388 126 p. 388 128 p. 388 130 p. 388 138 p. 389

Exercices supplémentaires en ligne (corrigés)

Calcul d'intégrale par calcul d'aire(s)

EX.01 EX.02 EX.03 EX.04 EX.05

Intégrales et primitives

EX.06 EX.07 EX.08 EX.09

Calcul d'aire à partir d'intégrale(s)

EX.10 EX.11 EX.12

Comparaisons d'intégrales

EX.13 EX.14

Suites et intégrales

EX.15 EX.16 EX.17 EX.18 EX.19

Types bac

EX.20 - Bac S 2016 EX.21 EX.22

Démonstration

Théo 7

Soient $f$ une fonction continue sur un intervalle $I$, $a$ un réel appartenant à $I$, et $F$ la fonction définie sur $I$ par $F(x) = \displaystyle\int_a^x f(t)\,\mathrm dt$.
Alors $F$ est l'unique primitive de $f$ s'annulant en $a$.

Preuve. Nous ne démontrons ce résultat que dans le cas où $f$ est positive et strictement croissante sur $I$ et $a$ est la borne inférieure de $I$.
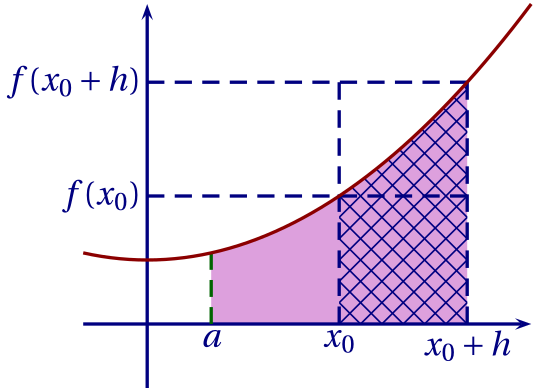
Dans ce cas, $F$ est la fonction qui à $x$ associe l'aire du domaine associé à la courbe de $f$ entre $a$ et $x$ (colorée en rose).

Pour $x_0 \in I$, et $h>0$, on peut encadrer $F(x_0+h) - F(x-0)$ (aire hachurée) par les aires de deux rectangles. \[\begin{aligned} &f(x_0)h \le F(x_0+h) - F(x_0) \le f(x_0+h)h& \\ \iff &f(x_0) \le \frac{F(x_0+h) - f(x_0)} h \le f(x_0+h)& \end{aligned}\] Donc, en passant à la limite: \[\begin{aligned} &\lim_{h\to 0} f(x_0) \le \lim_{h\to 0} \frac{F(x_0 + h) - F(x_0)}h \le \lim_{h\to0} f(x_0+h)& \\ \implies &f(x_0) \le F'(x_0) \le f(x_0)& \\ \implies &F'(x_0) = 0.& \end{aligned}\] On peut retrouver le même résultat quand $h < 0$. Donc pour tout $x_0\in I$, $F'(x_0) = f(x_0)$, ce qui prouve que $F$ est une primitive de $f$ sur $I$. Il est évident qu'elle s'annule en $a$.

retour