polynômes du second degré
Cours
retour
Avant de commencer, on pourra utilement réviser :
1. Polynômes
Déf. Soit $n$ un entier naturel, on appelle fonction polynôme (ou tout simplement polynôme) de degré $n$ toute fonction $P$ définie sur $\mathbb R$ par : \[ P(x) = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0,\] où $a_n$, $a_{n-1}$, …, $a_1$ et $a_0$ sont des constantes réelles, avec $a_n \neq 0$.
Ex.
- La fonction définie sur $\mathbb R$ par \[x\mapsto x^5 - 2x^3 + \frac 1 2x - 2\] est une fonction polynôme de degré 5.
- Les fonctions affines non constantes sont des fonctions polynômes de degré 1.
- Une fonction constante est une fonction polynôme de degré 0.
Déf. Une fonction polynôme de degré 2 (aussi appelée fonction trinôme) est donc une fonction $P$ définie sur $\mathbb R$ par \[ P(x) = ax^2 + bx + c,\] où $a$, $b$ et $c$ sont trois constantes réelles avec $a\neq 0$.
Déf.
$a$ est le coefficient de degré 2 (ou coefficient principal), $b$ est le coefficient de degré 1
et $c$ est le coefficient de degré $0$.
De même, $ax^2$ est le terme de degré 2, $bx$ le terme de degré 1 et $c$ le terme de degré 0 ou encore le terme constant.
Exercices
EX-01 EX-02 EX-03*
2. Forme canonique
Lemme Pour tous réels $a$ et $b$ : \[\begin{aligned} a^2 + 2ab &= (a+b)^2 - b^2\;;& \\ a^2 - 2ab &= (a-b)^2 - b^2.& \end{aligned}\]
Preuve
prop. & Déf.
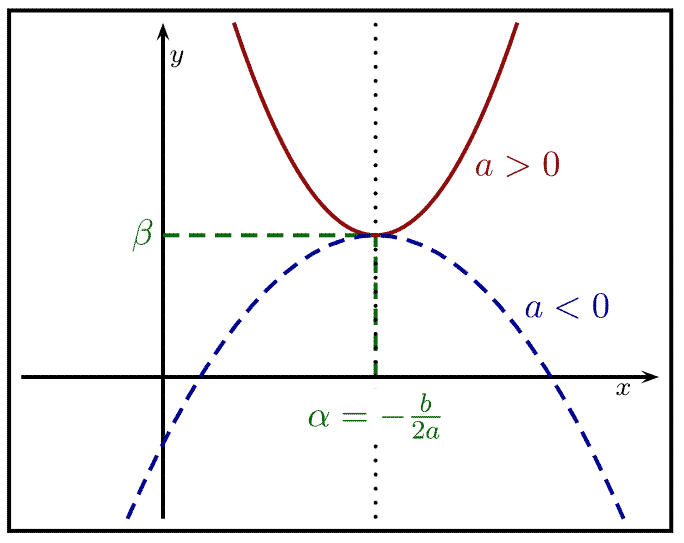
Soit $P:x\mapsto ax^2 + bx + c$ une fonction polynôme de degré 2.
Il existe un couple unique de réels $(\alpha;\beta)$ tels que:
\[P(x) = a\left(x -\alpha\right)^2 + \beta.\]
Cette écriture de $P(x)$ s'appelle la forme canonique de $P(x)$.
Rem. \[\alpha = -\frac b {2a}.\]
Ex.
-
\[\begin{aligned} P(x) &=x^2 + 6x + 1& \\ &=\underbrace{x^2+2(x)(3)}_{\text{lemme}} + 1& \\ &=(x+3)^2 - 3^2 + 1& \\ &=(x+3)^2 - 9 + 1& \\ &=\left(x-(-3)\right)^2 - 8.& \end{aligned}\] Cette dernière expression est la forme canonique de $P(x)$, avec $\alpha = -3$ et $\beta = -8$. -
\[\begin{aligned} Q(x)&=5x^2 - 3x + 1& \\ &=5\left(x^2 - \frac 3 5 x\right) + 1& \\ &=5\left[\underbrace{x^2 - (2)(x)\left(\frac 3{10}\right)}_{\text{lemme}}\right] + 1& \\ &=5\left[\left(x - \frac{3}{10}\right)^2 - \left(\frac 3 {10}\right)^2\right] + 1& \\ &=5\left(x - \frac 3 {10}\right)^2 - 5\times \frac 9 {100} + 1& \\ &=5\left(x - \frac 3 {10}\right)^2 - \frac{9}{20} + \frac{20}{20}& \\ &=5\left(x - \frac 3 {10}\right)^2 + \frac{11}{20}.& \end{aligned}\] On a donc la forme canonique de $Q(x)$ avec $\alpha = \frac 3{10}$ et $\beta = \frac{11}{20}$.
Preuve.
Exercices
EX-04 EX-05
3. Parabole
Prop. & déf. La courbe représentative d'une fonction polynôme de degré 2 est une parabole.
Ce résultat est admis.
Prop.
- Si $a>0$, $P$ est décroissante sur $\left]-\infty;-\frac{b}{2a}\right]$ et croissante sur $\left[-\frac b {2a};+\infty\right[$.
- Si $a < 0$, $P$ est croissante sur $\left]-\infty;-\frac{b}{2a}\right]$ et décroissante sur $\left[-\frac{b}{2a};+\infty\right[$.
Preuve.
$P(x) = a(x-\alpha)^2 + \beta$ avec $\alpha = -\dfrac{b}{2a}$.
Considérons $a>0$ et $x_1$ et $x_2$ deux réels quelconques de l'intervalle $\left]-\infty;-\frac b{2a}\right]$ Alors : \[x_1 < x_2 \implies x_1 - \frac b{2a} < x_2 - \frac b{2a}.\] Or $x_1$ et $x_2$ étant dans l'intervalle $\left]-\infty;-\frac b {2a}\right]$, les deux membres de cette inégalité sont négatifs.
La fonction carré est décroissante sur $]-\infty;0]$ donc : \[x_1 - \frac b{2a} < x_2 - \frac b {2a} \implies \left(x_1 - \frac b {2a}\right)^2 > \left(x_2 - \frac b {2a}\right)^2.\] Le coefficient $a$ étant ici strictement positif, multiplier par $a$ ne change pas l'ordre : \[\begin{aligned} \left(x_1 - \frac b {2a}\right)^2 &> \left(x_2 - \frac b {2a}\right)^2& \\ \implies a\left(x_1 - \frac b {2a}\right)^2 &> a\left(x_2 - \frac b {2a}\right)^2& \\ \implies a\left(x_1 - \frac b {2a}\right)^2 + \beta &> a\left(x_2 - \frac b {2a}\right)^2 + \beta& \\ \implies P(x_1) &> P(x_2).& \end{aligned}\] Sur l'intervalle $\left]-\infty;-\frac b{2a}\right]$, les images sont toujours dans l'ordre inverse des antécédents. C'est caractéristique d'une fonction décroissante.
On procède de manière analogue dans les autres cas.
Déf. Le point $S$ de la parabole ayant pour abscisse $-\dfrac b {2a}$ est appelé sommet de cette parabole.
Prop. La droite d'équation \[x=-\frac b {2a}\] est un axe de symétrie de la parabole.
Preuve.
4. Racines d'un polynôme de degré 2
Théo. Soit $P$ la fonction polynôme de degré 2 définie pour tout réel $x$ par $P(x)=ax^2+bx + c$.
- Si $\Delta<0$, $P(x)$ n'admet aucune racine et ne peut pas être factorisé.
- Si $\Delta =0$, $P(x)$ admet pour unique racine \[x_0=-\frac b {2a}\] et \[P(x)=a(x-x_0)^2.\]
- Si $\Delta >0$, alors $P(x)$ admet deux racines distinctes \[x_1 = \frac{-b-\sqrt{\Delta}}{2a}\quad\text{et}\quad x_2 = \frac{-b+\sqrt{\Delta}}{2a},\] et \[P(x) = a(x-x_1)(x-x_2).\]
Démo.
Si $\Delta > 0$ alors on peut utiliser la différence de deux carrés: \[\begin{aligned} P(x) &= a\left((x-\alpha)^2-\frac{\Delta}{4a^2}\right)& \\ &=a\left[(x-\alpha)^2 - \left(\frac{\sqrt{\Delta}}{2a}\right)^2\right]& \\ &=a\left((x-\alpha) - \frac{\sqrt{\Delta}}{2a}\right)\left((x-\alpha) + \frac{\sqrt{\Delta}}{2a}\right)& \\ &=a\left(x-\alpha - \frac{\sqrt{\Delta}}{2a}\right) \left(x - \alpha + \frac{\sqrt{\Delta}}{2a}\right)& \\ &=a\left(x - \frac{2a\alpha+\sqrt{\Delta}}{2a}\right) \left(x - \frac{2a\alpha - \sqrt{\Delta}}{2a}\right)& \end{aligned}\] Sachant que \[\alpha = -\dfrac{b}{2a} \implies 2a\alpha = -b.\] On obtient finalement \[P(x) = a\left(x - \frac{-b+\sqrt{\Delta}}{2a}\right) \left(x - \frac{-b-\sqrt{\Delta}}{2a}\right).\] De cette forme factorisée, on déduit que l'équation $P(x) = 0$ admet deux solutions \[x_1 = \frac{-b-\sqrt{\Delta}}{2a}\quad\text{et}\quad x_2 = \frac{-b+\sqrt{\Delta}}{2a}.\]
Si $\Delta = 0$ alors $\beta = -\dfrac{\Delta}{4a} = 0$.
Donc $P(x) = (x-\alpha)^2$.
Ce polynôme est donc déjà factorisé et \[\begin{aligned} P(x) &= 0& \\ \iff (x-\alpha)^2 &= 0& \\ \iff x - \alpha &= 0& \\ \iff x &= \alpha = -\frac b{2a}.& \end{aligned}\]
Si $\Delta < 0$, reprenons l'équation (1). \[P(x) = a\left((x-a)^2-\frac{\Delta}{4a^2}\right).\] Puisque $\Delta$ est négatif et $4a^2$ est positif, \[-\frac{\Delta}{4a^2}>0.\] De plus $(x-a)^2$ est aussi positif, donc \[(x-\alpha)^2 - \frac{\Delta}{4a^2} \ge -\frac{\Delta}{4a^2} > 0.\] Cette expression ne s'annule jamais, donc $P(x)$ non plus. L'équation $P(x) = 0$ est sans solution.
Prop. (somme et produit des racines). Soit $P(x)=ax^2+bx+c$ un polynôme admettant deux racines distinctes $x_1$ et $x_2$. Alors \[x_1 + x_2 = -\frac b a \quad\text{et}\quad x_1x_2 = \frac c a.\] Si $P(x)$ admet une unique racine $x_0$, le résultat précédent reste vrai en posant $x_0 = x_1 = x_2$.
Preuve.
Exercices
EX-06
EX-07
EX-08
EX-08*
EX-09*
EX-10
EX-11
(Avec la fonction exponentielle.)
EX-12
5. Signe d'une fonction polynôme de degré 2
Prop. Tableau de signe d'une fonction polynôme de degré 2 :
-
Si $P(x)$ n'a pas de racine :

-
Si $P(x)$ admet une racine unique $x_0$:

-
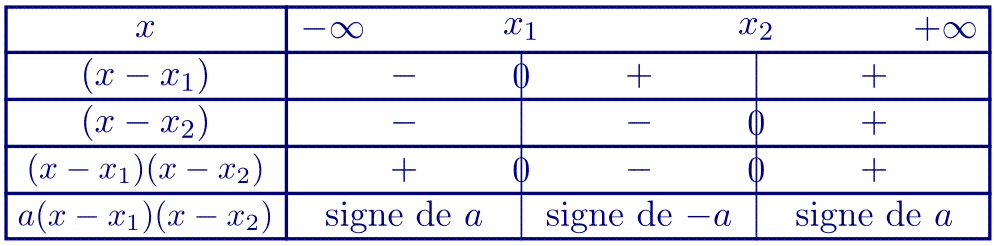
Si $P(x)$ admet deux racines distinctes $x_1$ et $x_2$ avec $x_1 < x_2$:

Preuve.
Si $P(x)$ admet la racine unique $x_0$, alors pour tout réel $x$ \[P(x) = a(x-x_0)^2.\] Le carré $(x-x_0)^2$ étant positif, $P(x)$ est donc du signe de $a$.
Si $P(x)$ admet deux racines $x_1$ et $x_2$ avec $x_1<x_2$, \[P(x) = a(x-x_1)(x-x_2).\] On peut alors établir le tableau de signes suivant
Exercices
EX-12*
(Avec la fonction exponentielle.)
EX-13
EX-14
(Sur l'ensemble de la leçon.)
EX-15
EX-16
EX-17
EX-18*