Exercice 1

1. Affirmation n° 1 fausse. En effet : \[f(-1) = 3\times (-1) - 7 = -3-7 = -10.\]

2. Affirmation n° 2 vraie. En effet : \[\begin{aligned} E &= (x-5)(x+1)& \\ &=x\cdot x + x\cdot 1 - 5\cdot x - 5\cdot 1& \\ &=x^2 + x - 5x - 5& \\ &=x^2 -4x - 5.& \end{aligned}\]

3. Affirmation n° 3 fausse. En effet : \[2^5 + 1 = 32 + 1 = 33.\] Or $33 = 3\times 11$, donc $33$ n'est pas premier.

4. Affirmation n° 4 vraie. En effet, la fréquence d'apparition de la face six est : \[\begin{aligned} &1 - \frac 3{15}-\frac4{15}-\frac5{15}-\frac2{15}-\frac1{15}& \\ =&\frac{15}{15}- \frac 3{15}-\frac4{15}-\frac5{15}-\frac2{15}-\frac1{15}& \\ =&\frac 0{15} =0.& \end{aligned}\]

5. Affirmation n° 5 vraie. Le triangle $ARS$ étant rectangle en $S$: \[\begin{aligned} \tan\widehat{ARS} &= \frac{AS}{RS}& \\ \iff \tan(26°) &= \frac{80}{RS}& \\ \iff RS \times \tan(26°) &= 80& \\ \iff RS &= \frac{80}{\tan(26°)}.& \end{aligned}\] Or, d'après la calculatrice $\dfrac{80}{\tan(26°)}\approx 164,02$.

6. Affirmation n° 6 fausse. Soit $ABCD$ un rectangle tel que $AB = 160$ et $BC = 95$. Alors le triangle $ABC$ est rectangle en $B$ et \[\begin{aligned} AC^2 &= AB^2 + BC^2& \\ \implies AC^2 &= 160^2 + 95^2& \\ \implies AC^2 &= 34\:625& \\ \implies AC &= \sqrt{34\:625}& \\ \implies AC &\approx 186,078.& \end{aligned}\] Donc $AC$ n'est pas exactement égale à 186 cm.

Exercice 2

Partie 1

1. {1 ; 2 ; 3 ; 4 ; 5 ; 6}.

2. La face 2 représente une issue parmi 6 issues équiprobables, donc \[P(A) = \frac 1 6.\]

3. Il y a 3 issues impaires (1, 3 et 5) parmi les six issues équiprobables donc \[P(B) = \frac36 = \frac12.\]

Partie 2

1. On ne peut pas obtenir 13 avec deux dés à six faces, donc \[P(C) = 0.\] $C$ est un événement impossible.

2.a. Tableau complété

dé rouge $\downarrow$, dé vert $\rightarrow$	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

2.b. liste des scores possibles (qui ne sont pas équiprobables):
{2 ; 3; 4; 5; 6; 7; 8 ; 9 ; 10 ; 11; 12}.

3.a. Parmi les 36 issues équiprobables du tableau, trois mènent à un score égal à 10. \[P(D) = \frac{3}{36} = \frac1{12}.\]

3.b. Les scores multiples de quatre sont quatre (3 issues), huit (5 issues) et douze (1 issue). Donc \[P(E) = \frac{3+5+1}{36} = \frac9{36} = \frac14.\]

3.c. Le score sera premier s'il est égal à 3, 5, 7 ou 11. Donc la probabilité d'obtenir un score premier est \[p_1 = \frac{3+4+6+2}{36} = \frac{15}{36} = \frac5{12}.\] La probabilité d'obtenir un nombre strictement plus grand que sept est \[p_2 = \frac{5+4+3+2+1}{36} = \frac{15}{36}=\frac5{12}.\] On a donc bien $p_1 = p_2$.

Exercice 3

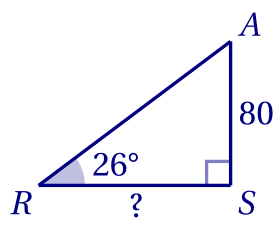
1. $\mathrm{EC} = 393 - 251 = 142\ \text{m}$.

2.a. (DB) et (EC) sont toutes deux parallèles à (AC), donc elles sont parallèles entre-elles.

2.b. Puisque (DB) et (EC) sont parallèles, le théorème de Thalès énonce que : \[\begin{aligned} \frac{\mathrm{AE}}{\mathrm{AD}} &= \frac{\mathrm{EC}}{\mathrm{BD}}& \\ \iff \frac{\mathrm{AE}}{51,25} &=\frac{142}{11,25}& \\ \iff \mathrm{AE} &=\frac{142\times 51,25}{11,25}& \\ \implies \mathrm{AE} &\approx 646,89\ \text{m}.& \end{aligned}\] Donc $\mathrm{DE} = \mathrm{AE} - \mathrm{DE} \approx 646,89 - 51,25 \approx 595,64$ mètres.
On peut donc bien arrondir la longueur DE à 596 mètres.

3. Durée du parcours : \[t = \frac d v = \frac{0,596}8 = 0,0745\ \text{h}.\] Soit, en minutes : \[0,0745 \times 60 = 4,47 \approx 4\ \text{min.}\] $55+4 = 59$, donc elle arrivera à environ 9 h 59.

4. Considérons le triangle ABD qui est rectangle en B: \[\begin{aligned} \mathrm{AD}^2&=\mathrm{AB}^2 + \mathrm{BD}^2& \\ \implies \mathrm{AB}^2 &= \mathrm{AD}^2 - \mathrm{BD}^2 = 51,25^2 - 11,25^2 = 2500.& \\ \implies \mathrm{AB} &=\sqrt{2500} = 50.& \end{aligned}\] Donc la pente est égale à : \[\frac{\mathrm{BD}}{\mathrm{AB}} = \frac{11,25}{50} = 0,225 = 22,5\:\text{%}.\]

Exercice 4

1. Tableau complété :

Nombre de journées de ski	2	6	10
Formule A	73 €	219 € (a)	365 € (c)
Formule B	127 €	201 € (b)	275 € (d)
Formule C	448,50 €	448,50 €	448,50 €

Calculs : (a) $36,5\times 6 = 219$, (b) $90+6\times 18,5 = 201$,
(c) $10\times 36,5 = 365$ et (d) $90+10\times 18,5 = 275$.

2.a. $h:\ x\mapsto 36,5x$.

2.b. $f$ correspond à la formule B, $g$ à la formule C et $h$ à la formule A.

2.c. On veut avoir \[\begin{aligned} h(x) &= f(x)& \\ \iff 36,5x &= 90 + 18,5x& \\ \iff 36,5x - 18,5 x &= 90& \\ \iff 18x &= 90& \\ \iff x &=\frac{90}{18}& \\ \iff x &= 5.& \end{aligned}\] Les formules A et B coûtent un même montant pour 5 journées de ski.

3.a. $(d_1)$ représente un coût fixe quel que soit le nombre de journées, donc $(d_1)$ représente la fonction $g$. $(d_2)$ passe par l'origine du repère, donc représente une fonction linéaire. $(d_2)$ représente donc la fonction $h$. Et $(d_3)$ représente la fonction $f$.

3.b. Marin pourra skier un maximum de 12 jours, en choisissant la formule B.

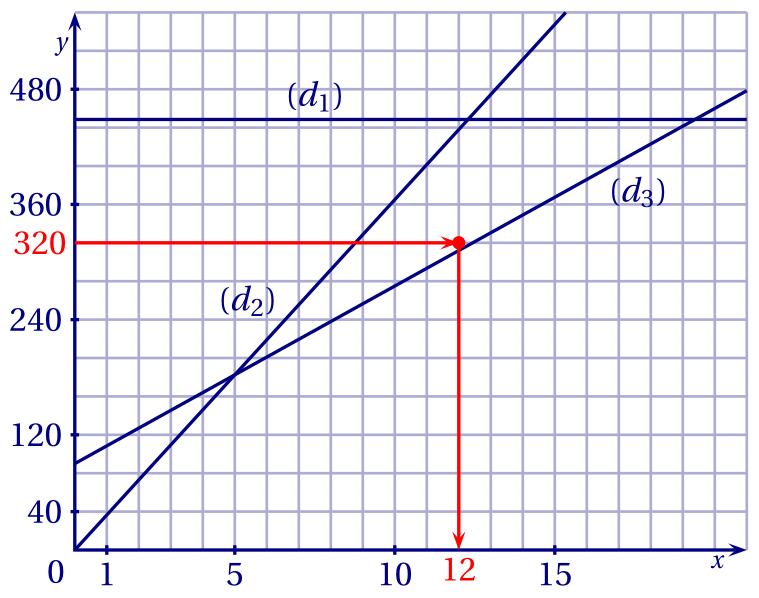
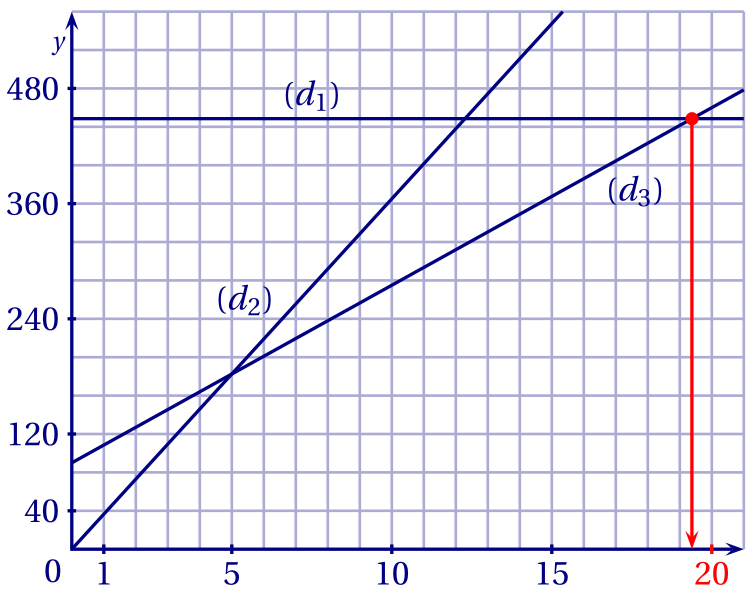
3.c. À partir de 20 journées de ski, la formule C est la plus avantageuse.

retour