EX. 01
retour
A.1.
D'après sa courbe, $f'$ est positive sur $]-\infty;0,5]$ (approximativement) puis négative sur
$[0,5;2,75]$ (approximativement) puis de nouveau positive sur $[0,75;+\infty[$.
Donc $f$ serait croissante sur $]-\infty;0,5]$, décroissante sur $[0,5;2,75]$ puis croissante sur
$[2,75;+\infty[$.
A.2. $f'$ semble croissante sur $]-\infty;-1]$, donc $f$ serait convexe sur cet intervalle. Puis $f'$ semble décroissante sur $[-1;2]$, donc $f$ serait concave sur cet intervalle. Enfin, $f'$ serait de nouveau croissante sur $[2;+\infty[$ donc $f$ serait à nouveau convexe sur cet intervalle.
B.1.a.
Pour tout réel $x\neq 0$, on a:
\[f(x) = \left(1-\frac 5x + \frac 6 {x^2}\right)x^2\mathrm e^{x}.\]
On sait que $\displaystyle\lim_{x\to+\infty}\dfrac5x = \displaystyle\lim_{x\to+\infty}\dfrac6{x^2} = 0$,
donc
$\displaystyle\lim_{x\to+\infty}\left(1-\dfrac5x+\dfrac6{x^2}\right)=1$.
De plus, $\displaystyle\lim_{x\to+\infty}x^2=\displaystyle\lim_{x\to+\infty}\mathrm e^x = +\infty$.
Donc en faisant le produit de ces limites, on obtient:
\[\lim_{x\to+\infty} f(x) = +\infty.\]
B.1.b.
On a encore :
\[f(x) = \left(1-\frac 5x + \frac 6 {x^2}\right)x^2\mathrm e^{x}.\]
D'une part, $\displaystyle\lim_{x\to-\infty}\dfrac5x = \displaystyle\lim_{x\to-\infty}\dfrac6{x^2} = 0$,
donc
$\displaystyle\lim_{x\to-\infty}\left(1-\dfrac5x+\dfrac6{x^2}\right)=1$.
D'autre part, on sait que quel que soit l'entier naturel $n$, $\displaystyle\lim_{x\to-\infty}x^n\mathrm e^x = 0$. Donc en particulier, $\displaystyle\lim_{x\to-\infty}x^2\mathrm e^x = 0$.
En réalisant le produit de ces deux limites, on obtient
\[\lim_{x\to-\infty} f(x) = 0.\]
B.2. $f=uv$ où $u$ et $v$ sont les deux fonction définies et dérivables sur $\mathbb R$ telles que \[\begin{aligned} u(x) &= x^2-5x\;;&\quad u'(x)&=2x - 5\;;& \\ v(x) &= \mathrm e^x\;;&\quad v'(x)&=\mathrm e^x.& \end{aligned}\] Donc $f$ est dérivable sur $\mathbb R$ et $f'=u'v + uv'$. Alors pour tout réel $x$: \[\begin{aligned} f'(x) &= (2x-5)\mathrm e^x + (x^2-5x+6)\mathrm e^x& \\ &= (2x - 5 + x^2 - 5x + 6)\mathrm e^x& \\ &=(x^2 - 3x + 1)\mathrm e^x.& \end{aligned}\]
B.3.
Le facteur $\mathrm e^x$ étant toujours strictement positif donc
le signe de $f'(x)$ est donné par le polynôme
$x^2 - 3x + 1$.
Son discriminant est $\Delta = (-3)^2 - 4\times 1 \times 1 = 9 - 4 = 5$.
Il est positif, donc ce polynôme admet deux racines:
\[x_1 = \frac{3 - \sqrt{5}}{2\times 1} = \frac{3-\sqrt 5}2
\quad\text{et}\quad
x_2 = \frac{3+\sqrt 5}{2\times 1} = \frac{3+\sqrt 5}2.\]
Son coefficient de degré 2 est 1, qui est positif, donc le polynôme est positif à l'extérieur de
ses racines.
Donc:
- sur l'intervalle $\left]-\infty;\dfrac{3-\sqrt 5}2\right]$, $f'$ est positive donc $f$ est croissante;
- sur l'intervalle $\left[\dfrac{3-\sqrt 5}2;\dfrac{3+\sqrt 5}2\right]$, $f'$ est négative donc $f$ est décroissante;
- sur l'intervalle $\left[\dfrac{3+\sqrt 5}2;+\infty\right[$, $f'$ est positive et donc $f$ est croissante.
4. On a: \[\begin{aligned} f(0) &= (0^2 - 5\times 0 + 6)\mathrm e^0 = 6\times 1 = 6\;;& \\ f'(0) &= (0^2 - 3\times 0 + 1)\mathrm e^0 = 1\times 1 = 1.& \end{aligned}\] Donc l'équation de $\mathscr T$ est \[ y = f'(0)(x-0) + f(0) \iff y = x + 6. \]
5.a. Étudions le signe de $f''(x)$ pour $x\in\mathbb R$. $\mathrm e^x$ est strictement positive, donc il dépend uniquement du produit $(x+1)(x-2)$.
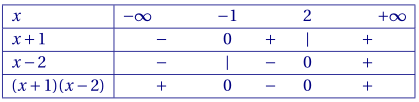
Sur $[-1;2]$, $f''$ est négative donc $f$ est concave.
5.b.
Nous venons de montrer que sur $[-1;2]$, la fonction $f$ est concave. Cela signifie que sur cet intervalle,
la courbe $\mathscr C$ est au dessous de ses tangentes, et donc en particulier au dessous de $\mathscr T$
dont l'équation est $y = x + 6$.
On a donc bien $f(x) \le x + 6$.
retour
code : 2997