Exercice 1
retour
1. Le vecteur $\overrightarrow{\mathrm{MN}}$ a pour coordonnées $\begin{pmatrix}0 - 1\\\frac12 - 1\\1-\frac34\end{pmatrix} =\begin{pmatrix}-1\\-\frac12\\ \frac14\end{pmatrix}$.
le vecteur $\overrightarrow{\mathrm{MP}}$ a pour coordonnées $\begin{pmatrix}1 - 1\\ 0 - 1\\ -\frac54 - \frac34\end{pmatrix} =\begin{pmatrix}0\\ -1\\ -2\end{pmatrix}$.
2. Figure ci-dessous.
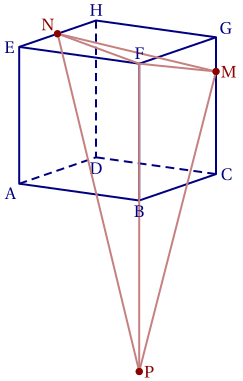
3. Si $M$, $N$ et $P$ étaient alignés, alors les vecteurs $\overrightarrow{\mathrm{MN}}$ et $\overrightarrow{\mathrm{MP}}$ seraient colinéaires et il existerait un réel $k$ tel que $\overrightarrow{\mathrm{MN}} = k\overrightarrow{\mathrm{MP}}$.
Or si l'on regarde les abscisses de ces deux vecteurs, il faudrait que $0k = 1$. C'est impossible, donc $M$, $N$ et $P$ ne sont pas alignés.
4.a. Le repère utilisé étant orthonormé, on a: \[\begin{aligned} \overrightarrow{\mathrm{MN}} \cdot \overrightarrow{\mathrm{MP}} &= -1\times 0 + \left(-\frac12\right)\times (-1) + \frac14\times(-2)& \\ &=0 + \frac12 -\frac12& \\ &= 0.& \end{aligned}\] Ce produit scalaire étant nul, $\overrightarrow{\mathrm{MN}}$ et $\overrightarrow{\mathrm{MP}}$ sont orthogonaux donc le triangle $\mathrm{MNP}$ est rectangle en $\mathrm M$.
4.b. On a : \[\begin{aligned} \mathrm{MN}^2 &= \overrightarrow{\mathrm{MN}}^2& \\ &= (-1)^2 + \left(-\frac12\right)^2 + \left(\frac14\right)^2& \\ &=1 + \frac14 + \frac1{16}& \\ &= \frac{21}{16}.& \end{aligned}\] Donc: $\mathrm{MN} = \sqrt{\dfrac{21}{16}} = \dfrac{\sqrt{21}}{\sqrt{16}} = \dfrac{\sqrt{21}}4$.
De même: \[\mathrm{MP}^2 = \overrightarrow{\mathrm{MP}}^2 =0^2 = (-1)^2 + (-2)^2 = 1 + 4 = 5.\] Donc $\mathrm{MP} = \sqrt{5}$.
Le triangle $\mathrm{MNP}$ étant rectangle en $\mathrm M$, son aire (en unité d'aire du repère) est: \[\mathscr A_{MNP} = \frac{\mathrm{MN}\times\mathrm{MP}}2 = \frac{\frac{\sqrt{21}}4\times\sqrt{5}}2 = \frac{\sqrt{21\times 5}}{4\times 2} = \frac{\sqrt{105}}8. \]
5.a. Le couple $\left(\overrightarrow{\mathrm{MN}},\overrightarrow{\mathrm{MP}}\right)$ forme une base du plan $(\mathrm{MNP})$.
Or : \[\begin{aligned} \vec n \cdot \overrightarrow{\mathrm{MN}} &= 5\times(-1) -8\times\left(-\frac12\right) + 4\times\frac14 = -5 + 4 + 1 = 0\;;& \\ \vec n\cdot\overrightarrow{\mathrm{MP}} &= 5 \times 0 - 8\times (-1) + 4\times(-2) = 0 + 8 - 8 = 0.& \end{aligned}\] $\vec n$ est donc orthogonal aux deux vecteurs directeurs du plan $(\mathrm{MNP})$. Il est donc normal à ce plan.
5.b. $\vec n$ étant normal au plan $(\mathrm{MNP})$, ce dernier admet pour équation cartésienne: \[5x - 8y + 4z + d = 0\] où la constante réelle $d$ reste à déterminer.
Or nous savons que $\mathrm N$ appartient à ce plan, donc que: \[\begin{aligned} 5x_N - 8y_N + 4z_N + d &= 0& \\ \iff 5\times 0 - 8\times\frac12 + 4\times 1 + d &= 0& \\ \iff -4 +4 + d &= 0& \\ \iff d &= 0.& \end{aligned}\] Donc une équation cartésienne du plan $(\mathrm{MNP})$ est: $\boxed{5x - 8y + 4z = 0.}$
6. Puisque la droite $d$ est orthogonal au plan $(\mathrm{MNP})$, elle est dirigée par $\vec n\begin{pmatrix}5\\-8\\4\end{pmatrix}$. Sachant de plus qu'elle passe par $\mathrm F(1;0;1)$, elle admet pour représentation paramétrique: \[d:\quad\begin{cases}x = 5t +1\\y = -8t\\z=4t + 1\end{cases},\quad t\in\mathbb R.\]
7. $\mathrm L$ n'est autre que le point d'intersection de la droite $d$ avec le plan $(\mathrm{MNP})$.
Puisqu'il est sur $d$, il existe un réel $t$ tel que $x_L = 5t+1$, $y_L = -8t$ et $z_L = 4t + 1$.
Mais $L$ est aussi sur le plan $(\mathrm{MNP})$, donc: \[\begin{aligned} 5x_L - 8y_L + 4z_L &= 0& \\ \iff 5(5t+1) - 8(-8t) + 4(4t+1) &= 0& \\ \iff 25t + 5 + 64t + 16t + 4 &= 0& \\ \iff 105t + 9 &= 0& \\ \iff t &=-\frac9{105} = -\frac{3}{35}.& \end{aligned}\] Donc: \[\begin{aligned} x_L &= 5t+1 = 5\times\left(-\frac{3}{35}\right) +1 = -\frac{3}{7} + \frac{7}{7} = \frac{4}{7}\;;& \\ y_L &= -8t = -8\times\left(-\frac3{35}\right) = \frac{24}{35}\;;& \\ z_L &= 4t + 1 = 4\times\left(-\frac3{35}\right) + 1 = -\frac{12}{35} + \frac{35}{35} = \frac{23}{35}.& \end{aligned}\]
8. Le vecteur $\overrightarrow{\mathrm{FL}}$ a pour coordonnées: \[\begin{pmatrix}\frac47 - 1\\ \frac{24}{35} -0 \\ \frac{23}{35}-1\end{pmatrix} =\begin{pmatrix}\frac47 - \frac77\\ \frac{24}{35} \\ \frac{23}{35}-\frac{35}{35}\end{pmatrix} =\begin{pmatrix}-\frac37\\ \frac{24}{35} \\ -\frac{12}{35}\end{pmatrix}. \] Donc \[\begin{aligned} \mathrm{FL}^2 &=\overrightarrow{\mathrm{FL}}^2& \\ &=\left(-\frac37\right)^2 + \left(\frac{24}{35}\right)^2 + \left(\frac{12}{35}\right)^2& \\ &=\frac{9}{49} + \frac{576}{1225} + \frac{144}{1225}& \\ &=\frac{9\times 25}{49\times 25} + \frac{576}{1225} + \frac{144}{1225}& \\ &=\frac{225 + 576 + 144}{1225}& \\ &=\frac{945}{1225}& \end{aligned}\] Alors: \[\mathrm{FL} = \sqrt{\frac{945}{1225}} = \frac{\sqrt{945}}{\sqrt{1225}}=\frac{3\sqrt{105}}{35}.\] Le volume du tétraèdre est donc (en unité de volume du repère): \[\mathscr V = \frac{\mathscr A_{MNP} \times \mathrm{FL}}3 =\frac{\frac{\sqrt{105}}8 \times \frac{\cancel{3}\sqrt{105}}{35}}{\cancel{3}} =\frac{\overset{3}{\cancel{105}}}{8\times \underset{1}{\cancel{35}}} =\frac{3}{8}. \]
retour
code : 2966