Exercice 4

retour

Partie A.

1.a. D'après la consigne, $P(G) = 0,2$.

1.b.

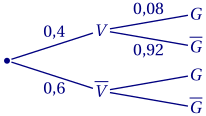
2. $P(G\cap V) = P(V) \times P_V(G) = 0,4 \times 0,08 = 0,032$.

3. On cherche $P_{\overline V}(G) = \dfrac{P(G\cap \overline V)}{P(\overline V)}$. Or: \[\begin{aligned} &P(G) = P(G\cap V) + P(G \cap \overline V)& \\ \implies &P(G \cap \overline V) = P(G) - P(G\cap V) = 0,2 - 0,032 = 0,168.& \end{aligned}\] Donc $P_{\overline V}(G) = \dfrac{P(G\cap \overline V)}{P(\overline V)} = \dfrac{0,168}{0,6} = 0,28$.

Partie B

1. Puisque ce sondage est assimilé à un tirage avec remise, $X$ suit la loi binomiale de paramètres $n$ (à déterminer) et $p=0,4$.

2.a. On cherche, à la calculatrice, $P(X = 15) \approx 0,123$.

2.b. On cherche, à la calculatrice, $P(X\ge 20) = 1 - P(X\le 19) \approx 1 - 0,870 \approx 0,130$.

2.c. On cherche, à la calculatrice,
$P(10 \le X \le 20) = P(X\le 20) - P(X \le 9)$
$\approx 0,926 - 0,016 \approx 0,910$.

retour

code : 2320