Exercice 3

retour

Partie A.

1. Arbre pondéré:

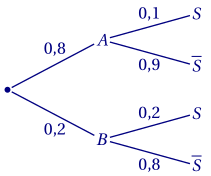
2.a. $P(B\cap \overline S) = P(B)\times P_{\overline S}(B) = 0,2\times 0,8 = 0,16$.

2.b. $P(\overline S) = P(A\cap \overline S) + P(B\cap \overline S) = 0,8 \times 0,9 + 0,16 = 0,88$.

3. On cherche: \[\begin{aligned} P_S(B) &= \frac{P(B\cap S)}{P(S)}& \\ &=\frac{P(B)\times P_B(S)}{1 - P(\overline S)}& \\ &=\frac{0,2\times 0,2}{1-0,88}& \\ &=\frac{0,04}{0,12}& \\ &=\frac 1 3& \\ &\approx 0,33.& \end{aligned}\]

Partie B.

1. Chaque achat ne comporte que deux issues (pesticides ou pas) et puisque l'on assimile cet achat à un tirage avec remise, chaque tirage est considéré indépendant des autres.
$X$ suit donc bien la loi binomiale de paramètres $n = 10$ et $p=0,88$.

2. D'après la calculatrice : $P(X=10) = 0,88^{10} \approx 0,28$.

3. D'après la calculatrice: $P(X\ge 8) = 1 - P(X \le 7) \approx 1 - 0,11 \approx 0,89$.

4. Le nombre moyen de boîtes est $\operatorname E(X) = np = 10 \times 0,88 = 8,8$.

retour

code : 2319