Exercice 2

retour

1.a. $\displaystyle\lim_{x\to 1} \mathrm e^x = \mathrm e$ (avec $\mathrm e>0$) et $\displaystyle\lim_{\substack{x\to1\\x< 1}} x - 1 = 0^-$. Donc par quotient de ces limites $\displaystyle\lim_{x\to1} f(x) = -\infty$.

1.b. On en déduit que la droite d'équation $x = 1$ est une asymptote verticale à $\mathscr C$.

2. $\displaystyle\lim_{x\to-\infty}\mathrm e^x = 0$ et $\displaystyle\lim_{x\to-\infty}x-1 = -\infty$ donc $\displaystyle\lim_{x\to-\infty} f(x) = 0$.

3.a. Pour tout $x\in]-\infty;1[$: \[\begin{aligned} f'(x) &= \frac{\mathrm e^x \cdot (x-1) - \mathrm e^x \cdot 1}{(x-1)^2}& \\ &=\frac{x\mathrm e^x - \mathrm e^x - \mathrm e^x}{(x-1)^2}& \\ &=\frac{(x-2)\mathrm e^x}{(x-1)^2}.& \end{aligned}\]

3.b. Les facteurs $(x-1)^2$ et $\mathrm e^x$ sont strictement positifs, et : \[x < 1 \implies x - 2 < 3 \implies x - 2 < 0.\] Donc pour tout réel $x\in]-\infty;1[$, $f'(x) < 0$. La fonction $f$ est donc strictement décroissante sur $]-\infty;1[$.

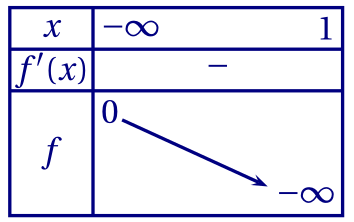
4.a. Le facteur $\mathrm e^x$ est strictement positif.
Puisque $x < 1$, $x- 1$ et donc $(x-1)^3$ est strictement négatif.
Le polynôme $x^2 - 4x + 5$ a pour discriminant $\Delta = (-4)^2 - 4\times 1\times 5 = -4$. Il est négatif, donc ce polynôme est toujours du signe de son coefficient de degré 2, donc positif.
Donc $f''(x)$ est négative pour tout réel $x\in]-\infty;1[$. La fonction $f$ est donc concave.

4.b. $f(0) = \dfrac{\mathrm e^0}{0-1} = -1$. $f'(0) = \dfrac{(0-2)\mathrm e^0}{(0-1)^2} = -2$.
L'équation réduite de la tangente $T$ a pour équation: \[\begin{aligned} y &= f'(0)(x-0) + f(0)& \\ \iff y &= -2x -1.& \end{aligned}\]

4.c. Puisque $f$ est concave, chacune de ses tangentes est située au dessus de sa courbe, donc en particulier $T$ est au dessus de $\mathscr C$.
Donc pour tout réel $x\in]-\infty;1[$: \[f(x) \le -2x - 1 \iff \frac{\mathrm e^x}{x-1} \le -2x-1\] Sachant que $x-1 < 0$: \[\frac{\mathrm e^x}{x-1} \le -2x-1 \iff \mathrm e^x \ge (-2x-1)(x-1).\]

5.a. La fonction $f$ est continue sur $]-\infty;1[$ avec $\displaystyle\lim_{x\to-\infty} f(x) = 0$ et $\displaystyle\lim_{x\to1} f(x) = -\infty$. Donc pour tout réel $k\in]-\infty;0[$, l'équation $f(x) =k$ admet une solution. C'est donc en particulier le cas pour $k=-2$.
De plus, $f$ est strictement décroissante, donc cette solution est unique.

5.b. À l'aide de la calculatrice, on peut constater que \[f(0,31) \approx -1,976\quad\text{et}\quad f(0,32) \approx -2,025.\] Donc $a\in]0,31\;;\;0,32[$.

retour

code : 1385