retour
Les parties A et B peuvent être traitées indépendamment
Partie A
Le plan est ramené à un repère orthogonal.
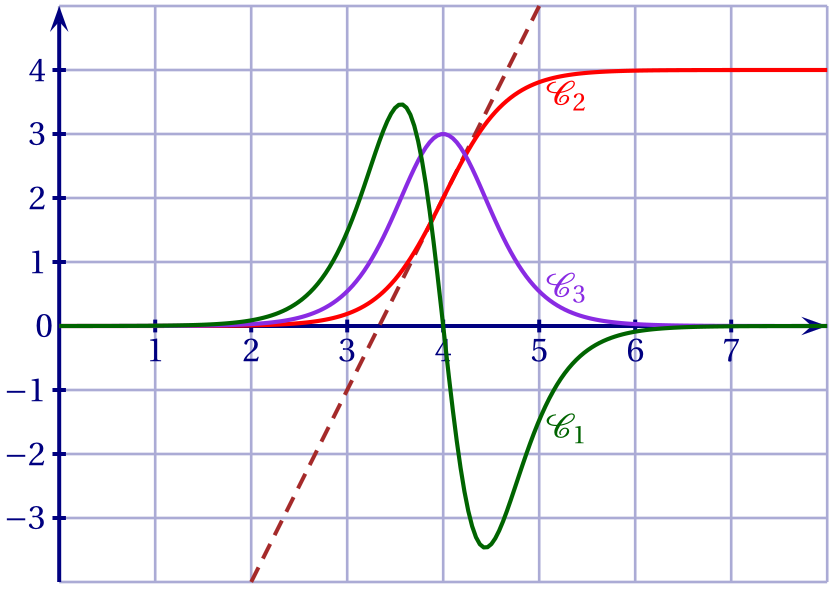
On a représenté ci-dessous la courbe d'une fonction $f$ définie et deux fois dérivable sur $\mathbb R$,
ainsi que celle de sa dérivée $f'$ et de sa dérivée seconde $f''$.
1.
Déterminer, en justifiant votre choix, quelle courbe correspond à quelle fonction.
Corrigé
Supposons que $f$ est représentée par la courbe $\mathscr C_2$. Alors $f$ est strictement croissante donc sa dérivée $f'$
est positive. Elle sera donc représentée par la courbe $\mathscr C_3$.
$f'$ est croissante sur $]-\infty;4]$ puis décroissante sur $[4;+\infty[$, donc sa dérivée doit être positive sur
$]-\infty;4]$ et négative sur $[4;+\infty[$. C'est bien le cas de la fonction représentée par la courbe $\mathscr C_1$.
2.
Déterminer, avec la précision permise par le graphique, le coefficient directeur de la tangente
à la courbe $\mathcal{C}_2$ au point d'abscisse 4.
Corrigé
La tangente semble passer par $A(3;-1)$ et $B(4;2)$. Son coefficient directeur devrait être:
\[\frac{y_B - y_A}{x_B - x_A} = \frac{2+1}{4-3} = 3.\]
3.
Donner avec la précision permise par le graphique,
l'abscisse de chaque point d'inflexion de la courbe $\mathcal{C}_1$.
Corrigé
La courbe $\mathscr C_1$ semble avoir un point d'inflexion d'abscisse voisine de $3,3$, un autre d'abscisse voisine de $4,5$ et
un troisième d'abscisse voisine de $5$.
Partie B
Soit un réel $k$ strictement positif.
On considère la fonction $g$ définie sur $\mathbb R$ par:
\[g(x) = \dfrac{4}{1 + \mathrm{e}^{-kx}}.\]
1.
Déterminer les limites de $g$ en $+\infty$ et en $-\infty$.
Corrigé
Puisque $k$ est positif, $-k$ est négatif donc:
\[\begin{aligned}
&\lim_{x\to+\infty} -kx = -\infty
\\
\implies &\lim_{x\to+\infty} \mathrm e^{-kx} = +0&
\\
\implies &\lim_{x\to+\infty} 1+\mathrm e^{-kx} = 1&
\\
\implies &\lim_{x\to+\infty} \frac 4{1+\mathrm e^{-kx}} =4.&
\end{aligned}\]
D'autre part:
\[\begin{aligned}
&\lim_{x\to-\infty} -kx = +\infty&
\\ \implies
&\lim_{x\to-\infty} \mathrm e^{-kx} = +\infty&
\\ \implies
&\lim_{x\to-\infty} 1+\mathrm e^{-kx} =+\infty&
\\
\implies
&\lim_{x\to-\infty} \frac 4{1+\mathrm e^{-kx}} = 0.&
\end{aligned}\]
2.
Prouver que $g'(0) = k$.
Corrigé
$g = 4\times\frac 1u$ où $u$ est la fonction strictement positive et dérivable sur $\mathbb R$
telle que:
\[u(x) = 1+\mathrm e^{-kt} \implies u'(x) = -k\mathrm e^{-kt}.\]
Donc $g$ est dérivable sur $\mathbb R$, de dérivée $4\times\left(-\frac{u'}{u^2}\right)$. Donc pour tout réel
$x$:
\[g'(x) = 4 \left(-\frac{-k\mathrm e^{-kx}}{(1+\mathrm e^{-kx})^2}\right)=\frac{4k\mathrm e^{-kx}}{(1+\mathrm e^{-kx})^2}.\]
Donc:
\[g'(0) = \frac{-k\mathrm e^{-k\times 0}}{(1+\mathrm e^{-k\times 0})^2}
=\frac{4k\times 1}{(1+1)^2} = \frac{4k}{4} = k.\]
3.
On admet le résultat ci-dessous obtenu avec un logiciel de calcul formel.
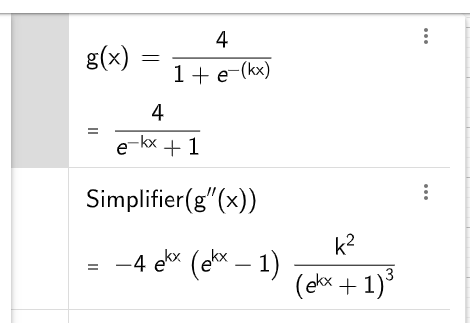
prouver que la courbe de $g$ admet un point d'inflexion au point d'abscisse 0.
Corrigé
D'après le logiciel de calcul formel:
\[\begin{aligned}
g''(x) &= -4\mathrm e^{kx}\left(\mathrm e^{kx} - 1\right)\frac{k^2}{\left(\mathrm e^{kx} + 1\right)^3}&
\\
&= 4\mathrm e^{kx}\left(1 - \mathrm e^{kx}\right)\frac{k^2}{\left(\mathrm e^{kx} + 1\right)^3}.&
\end{aligned}\]
Tous les facteurs sont strictement positifs, sauf $1 - \mathrm e^{-kx}$. Donc $g''(x)$ est du signe de
$1 - \mathrm e^{-kx}$.
Or
\[\begin{aligned}
&1- \mathrm e^{kx} = 0 \iff 1 = \mathrm e^{kx} \iff 0 = kx \iff 0 = x.&
\\
&1- \mathrm e^{kx} > 0 \iff 1 > \mathrm e^{kx} \iff 0 > kx \iff 0 > x.&
\end{aligned}\]
Donc sur $]-\infty;0]$, $g''$ est négative et donc $g$ est concave. Sue $[0;+\infty[$, $g''$ est positive et donc $g$ est convexe.
La courbe de $g$ admet donc un unique point d'inflexion, d'abscisse $0$.