AP-06/11

retour

Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.

Le graphique ci-contre donne la représentation graphique $\mathcal{C}_f$ dans un repère orthogonal d'une fonction $f$ définie et dérivable sur $\mathbb R$.

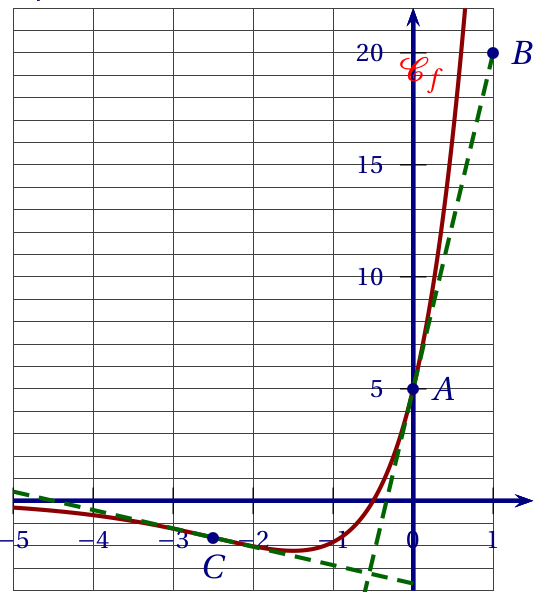
On donne les points $A$ de coordonnées $(0;5)$ et $B$ de coordonnées $(1;20)$.

Le point $C$ est le point de la courbe $\mathcal{C}_f$ ayant pour abscisse $-2,5.$

La droite $(AB)$ est la tangente à la courbe $\mathcal{C}_f$ au point $A$.

Les questions 1 à 3 se rapportent à cette même fonction $f$.

1. On peut affirmer que:
a. $f'(-0,5) = 0$;
b. si $x \in ]-\infty;-0,5[$, alors $f'(x) < 0$;
c. $f'(0) = 15$;
d. la fonction dérivée $f'$ ne change pas de signe sur $\mathbb R$.

Corrigé

Réponse c. Si $f'(-0,5) = 0$, alors $\mathscr C_f$ doit admettre une tangente horizontale au point d'abscisse $-0,5$. Ce n'est pas le cas.
Si $f'<0$ sur $]-\infty;-0,5[$, alors $f$ doit être décroissante sur tout cet intervalle. Ce n'est pas le cas.
$f'(0)$ est le coefficient directeur de la droite $(AB)$. Or ce dernier est égal à \[\frac{y_B - y_A}{x_B - x_A} = \frac{20 - 5}{1 - 0} = 15.\]
$f$ est décroissante puis croissante, donc $f'$ change de signe.

2. On admet que la fonction $f$ représentée ci-dessus est définie sur $\mathbb R$ par \[f(x) = (ax + b)\mathrm{e}^x,\] où $a$ et $b$ sont deux nombres réels et que sa courbe coupe l'axe des abscisses en son point de coordonnées $(-0,5;0)$.
On peut affirmer que:
a. $a = 10$ et $b = 5$;
b. $a = 2,5$ et $b = -0,5$;
c. $a = -1,5$ et $b = 5$;
d. $a = 0$ et $b = 5$.

Corrigé

Réponse a. Puisque $A\in\mathscr C_f$ on a \[\begin{aligned} &f(0) = 5& \\ \iff &(a\times 0 + b)\mathrm e^0 = 5& \\ \iff &b\times 1 = 5& \\ \iff &b = 5.& \end{aligned}\] On sait aussi que $f'(0) = 15$.
Or pour tout réel $x$: \[\begin{aligned} f'(x) &= a\mathrm e^x + (ax+b)\mathrm e^x& \\ &= (ax + a + b)\mathrm e^x& \\ &= (ax+a+5)\mathrm e^x.& \end{aligned}\] Donc \[\begin{aligned} &f'(0) = 15& \\ \iff &(a+5)\mathrm e^0 = 15& \\ \iff &(a+5)\times 1= 15& \\ \iff &a= 10.& \end{aligned}\]

3. On admet que la dérivée seconde de la fonction $f$ est définie sur $\mathbb R$ par: \[f''(x) = (10x + 25)\mathrm{e}^x.\] On peut affirmer que:
a. La fonction $f$ est convexe sur $\mathbb R$;
b. La fonction $f$ est concave sur $\mathbb R$;
c. Le point C est l'unique point d'inflexion de $\mathcal{C}_f$;
d. $\mathcal{C}_f$ n'admet pas de point d'inflexion.

Corrigé

Réponse c. Puisque $\mathrm e^x>0$, le signe de $f''(x)$ est entièrement déterminé par celui de $10x+25$.
Or : \[10x + 25 = 0 \iff x = -\frac{25}{10} = -\frac 5 2.\] Le coefficient directeur est positif, donc $f''$ est strictement négative sur $\left]-\infty;-\frac 5 2\right[$, nulle en $-\frac 5 2$ et strictement positive sur $\left]-\frac 5 2;+\infty\right[$.
La fonction $f$ n'est convexe que sur $\left[-\frac 5 2;+\infty\right[$ et concave que sur $\left]-\infty;-\frac 5 2\right]$. Elle change de convexité une seule fois, donc admet un unique point d'inflexion.

4. On considère deux suites $\left(U_n\right)$ et $\left(V_n\right)$ définies sur $\mathbb N$ telles que:

pour tout entier naturel $n$, $U_n \leqslant V_n$;
$\displaystyle\lim_{n \to+ \infty} V_n= 2$.

On peut affirmer que:
a. la suite $\left(U_n\right)$ converge;
b. pour tout entier naturel $n$, $V_n \leqslant 2$;
c. la suite $\left(U_n\right)$ diverge;
d. la suite $\left(U_n\right)$ est majorée.

Corrigé

Réponse d. La suite $(V_n)$ est convergente, donc elle est bornée. Il existe donc un réel $M$ tel que, pour tout entier naturel $n$, $V_n \le M$.
Donc pour tout entier naturel $n$: \[U_n \le V_n \le M.\] $M$ est un majorant de la suite $(U_n)$.
La suite $(U_n)$ peut être divergente, mais elle peut aussi converger vers un réel inférieur ou égal à 2.
La suite $(V_n)$ n'est pas nécessairement croissante, donc elle peut admettre des termes supérieurs à sa limite.

retour

code : 892