AP-06/10
retour
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée.
Soit $\left(u_n\right)$ une suite définie pour tout entier naturel $n$ et telle que pour tout entier naturel $n$, \[\dfrac12 < u_n \le \dfrac{3n^2 + 4n + 7}{6n^2 + 1}.\]
Affirmation 1. $\displaystyle\lim_{n \to + \infty} u_n =\dfrac12$.
Pour tout entier naturel $n$ différent de $0$: \[\frac{3n^2 + 4n + 7}{6n^2+1} =\frac{\cancel{n^2}\left(\frac{3n^2}{n^2} + \frac{4n}{n^2} + \frac{7}{n^2}\right)}{\cancel{n^2}\left(\frac{6n^2}{n^2}+\frac1{n^2}\right)} =\frac{3 + \frac4n + \frac7{n^2}}{6 + \frac 1 {n^2}}.\] Or $\displaystyle\lim_{n\to+\infty} \dfrac 4 n = \displaystyle\lim_{n\to+\infty} \dfrac{7}{n^2} = 0$ donc $\displaystyle\lim_{n\to+\infty}3+\dfrac4{n}+\dfrac{7}{n^2} = 3$.
D'autre part : $\displaystyle\lim_{n\to+\infty} \frac 1{n^2} = 0$ donc $\displaystyle\lim_{n\to+\infty} 6 + \dfrac 1{n^2} = 6$.
Donc : $\displaystyle\lim_{n\to+\infty} \frac{3 + \frac4n + \frac7{n^2}}{6 + \frac 1 {n^2}} = \dfrac 36 = \dfrac 12$.
La suite $(u_n)$ est donc encadrée par deux suites qui tendent vers $\dfrac 12$. Elle tend donc elle-même vers cette valeur.
Soit $f$ une fonction définie et dérivable sur l'intervalle $[-4;4]$.
La représentation graphique $\mathcal{C}_{f'}$ de sa fonction dérivée $f'$ est donnée ci-dessous.
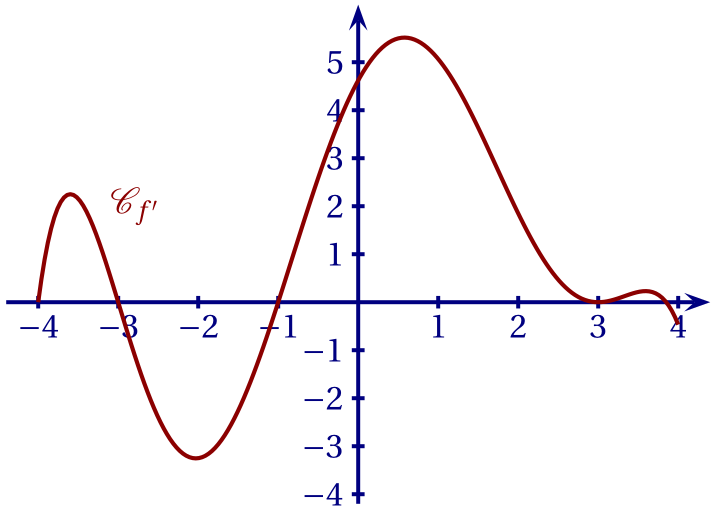
Pour que la fonction $f$ soit convexe sur $[-1;3]$, il faudrait que sa fonction dérivée $f'$ soit croissante sur cet intervalle. Ce n'est clairement pas le cas.
On considère la fonction $g$ définie sur $\mathbb R$ par: \[g(x)=5 x \mathrm e^{-x}.\] On note $C_{g}$ la courbe représentative de $g$ dans un repère orthonormé.
Affirmation 3: L'axe des abscisses est une asymptote horizontale à la courbe $C_{g}$.
On sait que: $\displaystyle\lim_{x\to+\infty} \dfrac{\mathrm e^x}x = +\infty$.
On en déduit que $\displaystyle\lim_{x\to+\infty}\dfrac{x}{\mathrm e^x} = \displaystyle\lim_{x\to+\infty}x\mathrm e^{-x}= 0$.
Donc $\displaystyle\lim_{x\to+\infty} 5x\mathrm e^{-x} = 0$.
L'axe des abscisses est bien une asymptote horizontale à $C_g$ en $+\infty$.
On considère les suites $\left(u_{n}\right)$, $\left(v_{n}\right)$ et $\left(w_{n}\right)$, telles que, pour tout entier naturel $n$: \[u_{n} \leqslant v_{n} \leqslant w_{n}.\] De plus, la suite $\left(u_{n}\right)$ converge vers $-1$ et la suite $\left(w_{n}\right)$ converge vers 1.
Affirmation 4 : La suite $\left(v_{n}\right)$ converge vers un nombre réel $\ell$ appartenant à l'intervalle $[-1 ; 1]$.
Proposons un contre-exemple: Pour tout entier naturel $n$, $u_n = -1-\dfrac 1{n+1}$, $w_n = 1+\dfrac1{n+1}$ et $v_n = (-1)^n$.
Ces suites vérifient bien les conditions : $(u_n)$ converge vers $-1$, $(w_n)$ converge vers $1$ et pour tout entier naturel $n$: \[-1-\dfrac1{n+1} \le -1 \le (-1)^n \le 1 \le 1+\dfrac1{n+1}.\] Cependant, la suite $(v_n)$ ne converge pas.
On suppose de plus que la suite $\left(u_{n}\right)$ est croissante et que la suite $\left(w_{n}\right)$ est décroissante.
Affirmation 5 : Pour tout entier naturel $n$, on a alors: \[u_{0} \leqslant v_{n} \leqslant w_{0}.\]
Pour tout entier naturel $n$, on a: \[u_n \le v_n \le w_n.\] Mais $(u_n)$ est croissante, donc pour tout entier naturel $n$: $u_0 \le u_n$.
De même, $(w_n)$ est décroissante donc pour tout entier naturel $n$: $w_n \le w_0$.
On a donc: \[u_0 \le u_n \le v_n \le w_n \le w_0 \implies u_0 \le v_n \le w_0.\]
retour
code : 891