AP-06/09

retour

Léa passe une bonne partie de ses journées à jouer à un jeu vidéo et s'intéresse aux chances de victoire de ses prochaines parties.
Elle estime que si elle vient de gagner une partie, elle gagne la suivante dans 70 % des cas.
Mais si elle vient de subir une défaite, d'après elle, la probabilité qu'elle gagne la suivante est de 0,2.
De plus, elle pense avoir autant de chance de gagner la première partie que de la perdre.
On s'appuiera sur les affirmations de Léa pour répondre aux questions de cet exercice.
Pour tout entier naturel $n$ non nul, on définit les évènements suivants :

$G_n$ : «Léa gagne la $n$-ième partie de la journée»;
$D_n$ : «Léa perd la $n$-ième partie de la journée».

Pour tout entier naturel $n$ non nul, on note $g_n$ la probabilité de l'évènement $G_n$.
On a donc $g_1 = 0,5$.

1. Quelle est la valeur de la probabilité conditionnelle $P_{G_1}\left(D_2\right)$?

Corrigé

$P_{G_1}(D_2) = 1 - P_{G_1}(G_2) = 1 - 0,7 = 0,3$.

2. Recopier et compléter l'arbre des probabilités ci-dessous qui modélise la situation pour les deux premières parties de la journée:

Corrigé

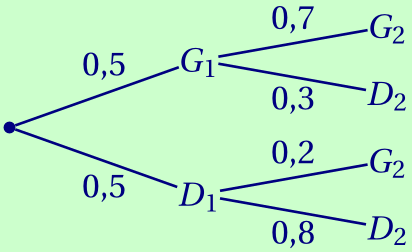
Arbre complété :

3. Calculer $g_2$.

Corrigé

\[\begin{aligned} g_2 = P(G_2) &= P(G_2\cap G_1) + P(G_2\cap D_1)& \\ &=P(G_1)\times P_{G_1}(G_2) + P(D_1)\times P_{D_1}(G_2)& \\ &=0,5 \times 0,7 + 0,5 \times 0,2& \\ &=0,35 + 0,10& \\ &=0,45.& \end{aligned}\]

4. Soit $n$ un entier naturel non nul.

a. Recopier et compléter l'arbre des probabilités ci-dessous qui modélise la situation pour les $n$-ième et $(n + 1)$-ième parties de la journée.

Corrigé

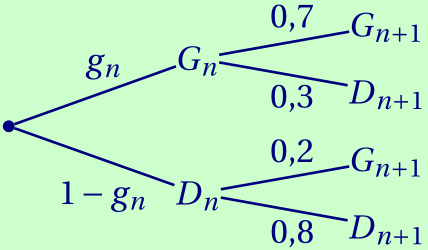
Arbre complété :

b. Justifier que pour tout entier naturel $n$ non nul, \[g_{n+1} = 0,5g_n + 0,2.\]

Corrigé

\[\begin{aligned} P(G_{n+1}) &= P(G_{n+1}\cap G_n) + P(G_{n+1}\cap D_n)& \\ &=P(G_n) \times P_{G_n}(G_{n+1}) + P(D_n)\times P_{D_n}(G_{n+1})& \\ &=0,7g_n + 0,2(1-g_n)& \\ &=0,7g_n + 0,2 - 0,2g_n& \\ &=0,5g_n + 0,2.& \end{aligned}\]

5. Pour tout entier naturel $n$ non nul, on pose $v_n = g_n - 0,4$.

a. Montrer que la suite $\left(v_n\right)$ est géométrique.
On précisera son premier terme et sa raison.

Corrigé

Pour tout entier naturel $n$ non nul: \[v_{n+1} = g_{n+1} - 0,4 =0,5g_n + 0,2 - 0,4 =0,5g_n - 0,2.\] Or: \[v_n = g_n - 0,4 \iff v_n + 0,4 = g_n\] Donc: \[\begin{aligned} &0,5g_n - 0,2 = 0,5(v_n + 0,4) - 0,2& \\ &= 0,5v_n + 0,2 - 0,2 = 0,5v_n.& \end{aligned}\] La suite $(v_n)$ est donc géométrique de raison $q=0,5$. Son premier terme est \[v_1 = g_1 - 0,4 = 0,5 - 0,4 = 0,1.\]

b. Montrer que, pour tout entier naturel $n$ non nul : \[g_n = 0,1 \times 0,5^{n-1} + 0,4.\]

Corrigé

On a donc, pour tout entier naturel $n$ non nul: \[v_n = v_1q^{n-1} = 0,1\times 0,5^{n-1}.\] Donc pour tout entier naturel $n$ non nul: \[g_n = v-n + 0,4 = 0,1\times 0,5^{n-1} + 0,4.\]

6. Étudier les variations de la suite $\left(g_n\right)$.

Corrigé

Puisque $0,5\in]0;1[$, la suite $(0,5^n)$ est décroissante. Donc pour tout entier naturel $n$ non nul : \[\begin{aligned} &0,5^{n-1} > 0,5^{n}& \\ \iff &0,1\times 0,5^{n-1} > 0,1\times 0,5^{n}& \\ \iff &0,1\times 0,5^{n-1} + 0,4 > 0,1\times 0,5^n + 0,4& \\ \iff &g_n > g_{n+1}.& \end{aligned}\] La suite $(g_n)$ est donc décroissante.

7. Donner, en justifiant, la limite de la suite $\left(g_n\right)$.
Interpréter le résultat dans le contexte de l'énoncé.

Corrigé

Puisque $0,5\in]-1;1[$, $\displaystyle\lim_{n\to+\infty} 0,5^{n-1} = 0$.
Donc $\displaystyle\lim_{n\to+\infty} 0,1\times 0,5^{n-1} = 0$.\\ Et donc finalement : $\displaystyle\lim_{n\to+\infty} 0,1\times 0,5^{n-1} + 0,4 = 0,4$. La suite $(g_n)$ converge donc vers $0,4$.
À long terme, Léa a 40% de chances de gagner une partie.

8. Déterminer, par le calcul, le plus petit entier $n$ tel que \[g_n - 0,4 \le 0,001.\]

Corrigé

$n$ doit vérifier la relation: \[\begin{aligned} &g_n - 0,4 \le 0,001& \\ \iff &0,1\times 0,5^{n-1} + \cancel{0,4} - \cancel{0,4} \le 0,001& \\ \iff &0,5^{n-1} \le \frac{0,001}{0,1}& \\ \iff & 0,5^{n-1} \le 0,01& \\ \iff &\ln\left(0,5^{n-1}\right) \le \ln(0,01)& \\ \iff &(n-1)\ln(0,5) \le \ln(0,01)& \end{aligned}\] On note ici que $\ln(0,5)$ est négatif, donc que diviser par $\ln(0,5)$ change le sens de l'inégalité. \[\begin{aligned} &(n-1)\ln(0,5) \le \ln(0,01)& \\ \iff &n - 1 \ge \frac{\ln(0,01)}{\ln(0,5)}& \\ \iff &n \ge \frac{\ln(0,01)}{\ln(0,5)}+1& \end{aligned}\] Or $\dfrac{\ln(0,01)}{\ln(0,5)}+1 \approx 7,64$. Donc $n = 8$.

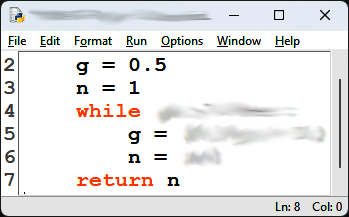
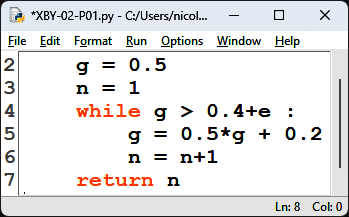
9. Recopier et compléter les lignes 4, 5 et 6 de la fonction suivante, écrite en langage Python, afin qu'elle renvoie le plus petit rang à partir duquel les termes de la suite $\left(g_n\right)$ sont tous inférieurs ou égaux à $0,4 + e$, où $e$ est un nombre réel strictement positif.

Corrigé

Listing complété:

retour

code : 890