AP-06/08
retour
On considère la fonction $f$ définie sur $]0;+\infty[$ par
\[f(x) = x^2 - x \ln (x).\]
On admet que $f$ est deux fois dérivable sur $]0;+\infty[$.
On note $f'$ la fonction dérivée de la fonction $f$ et $f''$ la fonction dérivée de la fonction $f'$.
Partie A : Étude de la fonction $f$
1. Déterminer les limites de la fonction $f$ en $0$ et en $+\infty$.
De plus : $\displaystyle\lim_{x\to0}x^2 = 0$.
Donc en sommant ces deux limites : $\displaystyle\lim_{x\to0} x^2 - x\ln(x) = 0$.
Donc : $\displaystyle\lim_{x\to+\infty} 1 - \dfrac{\ln(x)}{x} = 1$.
D'autre part : $\displaystyle\lim_{x\to+\infty} x^2 = +\infty$.
Donc par produit de ces deux limites : $\displaystyle\lim_{x\to+\infty} x^2\left(1-\dfrac{\ln(x)}x\right) = +\infty$.
2. Pour tout réel $x$ strictement positif, calculer $f'(x)$.
3. Montrer que pour tout réel $x$ strictement positif: \[f''(x) = \dfrac{2x - 1}{x}.\]
4.
Étudier les variations de la fonction $f'$ sur $]0;+\infty[$, puis dresser le tableau des variations de la fonction $f'$ sur $]0;+\infty[$.
On veillera à faire apparaître la valeur exacte de l'extremum de la fonction $f'$ sur $]0;+\infty[$.
Les limites de la fonction $f'$ aux bornes de l'intervalle de définition ne sont pas attendues.
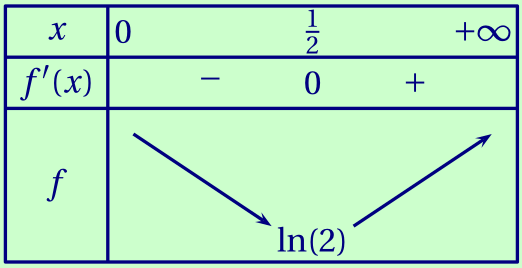
avec $f'\left(\dfrac12\right)=2\times\dfrac12 - \ln\left(\dfrac12\right)-1 = 1+\ln(2)-1 = \ln(2)$.
5. Montrer que la fonction $f$ est strictement croissante sur $]0;+\infty[$.
Partie B : Étude d'une fonction auxiliaire pour la résolution de l'équation $f(x) = x$
On considère dans cette partie la fonction $g$ définie sur $]0;+\infty[$ par \[g(x) = x - \ln (x).\] On admet que la fonction $g$ est dérivable sur $]0;+\infty[$, on note $g'$ sa dérivée.
1.
Pour tout réel strictement positif, calculer $g'(x)$, puis dresser le tableau des variations de la fonction $g$.
Les limites de la fonction $g$ aux bornes de l'intervalle de définition ne sont pas attendues.
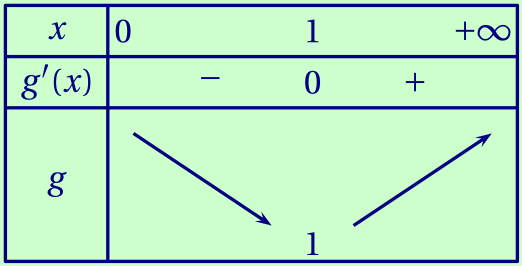
avec $g\left(1\right)=1-\ln(1) = 1 - 0 = 1$.
2.
On admet que 1 est l'unique solution de l'équation $g(x) = 1$.
Résoudre, sur l'intervalle $]0;+\infty[$, l'équation $f(x) = x$.
C'est donc aussi l'unique solution de l'équation $f(x) = x$.
Partie C : Étude d'une suite récurrente
On considère la suite $\left(u_n\right)$ définie par $u_0 = \dfrac12$ et pour tout entier naturel $n$, \[u_{n+1} = f\left(u_n\right) = u_n^2 - u_n \ln \left(u_n\right).\]
1. Montrer par récurrence que pour tout entier naturel $n$: \[\dfrac12 \leqslant u_n \leqslant u_{n+1} \leqslant 1.\]
$u_0 = \dfrac 12$ et $u_1 = \left(\dfrac12\right)^2-\dfrac12\ln\left(\dfrac12\right) \approx 0,6$. Donc $\mathcal A(0)$ est vraie.
Supposons, pour un entier naturel $n$ fixé quelconque, que $\mathcal A(n)$ est vraie. On a donc: \[\frac 12 \le u_n \le u_{n+1} \le 1.\] Or la fonction $f$ est strictement croissante sur $\left[\dfrac12;+\infty\right[$. Donc : \[\begin{aligned} &\frac12 \le u_n \le u_{n+1} \le 1& \\ \implies &f\left(\dfrac12\right) \le f(u_n) \le f(u_{n+1}) \le f(1)& \\ \implies &f\left(\dfrac12\right) \le u_{n+1} \le u_{n+2} \le f(1)& \end{aligned}\] Or on sait déjà que $f\left(\dfrac 12\right) \approx 0,6$ donc $f\left(\dfrac 12\right) \ge \dfrac12$ et que $f(1) = 1$. Donc: \[\begin{aligned} &f\left(\dfrac12\right) \le u_{n+1} \le u_{n+2} \le f(1)& \\ \implies &\dfrac 12 \le f\left(\dfrac12\right) \le u_{n+1} \le u_{n+2} \le f(1) \le 1& \\ \implies &\dfrac 12 \le u_{n+1} \le u_{n+2} \le 1.& \end{aligned}\] Donc $\mathcal A(n+1)$ est aussi vraie.
Initialisée et héréditaire, $\mathcal A(n)$ est donc vraie pour tout entier naturel $n$ par récurrence.
2. Justifier que la suite $\left(u_n\right)$ converge.
La suite $(u_n)$ est donc convergente.
3.
On appelle $\ell$ la limite de la suite $\left(u_n\right)$ et on admet que $\ell$ vérifie l'égalité $f(\ell) = \ell$.
Déterminer la valeur de $\ell$.
retour
code : 889