AP-06/07
retour
Pour chacune des affirmations suivantes, préciser si elle est vraie ou fausse puis justifier la réponse donnée.
Affirmation 1: Toute suite décroissante et minorée par 0 converge vers 0.
Corrigé
Affirmation fausse.
Il est vrai que toute suite décroissante et minorée par $0$ converge, mais pas nécessairement
vers 0.
Pour s'en convaincre, on peut proposer comme contre-exemple la suite définie sur $\mathbb N^*$ par \[u_n = 1+\frac 1n.\] Plus $n$ est grand, plus $\frac 1n$ est petit, donc $(u_n)$ est décroissante, et puisque $u_n$ est la somme de deux nombres strictement positif, $u_n$ est strictement positif. Donc $(u_n)$ est minorée par $0$.
Cependant : \[\displaystyle\lim_{n\to+\infty} \dfrac 1n = 0 \implies \lim_{n\to +\infty} 1 + \frac 1 n = 1.\]
Pour s'en convaincre, on peut proposer comme contre-exemple la suite définie sur $\mathbb N^*$ par \[u_n = 1+\frac 1n.\] Plus $n$ est grand, plus $\frac 1n$ est petit, donc $(u_n)$ est décroissante, et puisque $u_n$ est la somme de deux nombres strictement positif, $u_n$ est strictement positif. Donc $(u_n)$ est minorée par $0$.
Cependant : \[\displaystyle\lim_{n\to+\infty} \dfrac 1n = 0 \implies \lim_{n\to +\infty} 1 + \frac 1 n = 1.\]
On considère une suite $\left(u_n\right)$ définie sur $\mathbb N$ telle que, pour tout entier $n$, on a \[u_n \le \dfrac{-9^n + 3^n}{7^n}.\] Affirmation 2 : $\displaystyle\lim_{n \to + \infty} u_n =- \infty$.
Corrigé
Affirmation vraie. Remarquons d'abord que
\[\frac{-9^n+3^n}{7^n} = \frac{-9^n}{7^n} + \frac{3^n}{7^n} = -\left(\frac 9 7\right)^n + \left(\frac 3 7\right)^n.\]
Or :
\[\begin{aligned}
\frac 9 7 > 1 \implies
&\lim_{n\to+\infty} \left(\frac97\right)^n = +\infty&
\\
&\implies \lim_{n\to+\infty} -\left(\frac97\right)^n = -\infty.&
\end{aligned}\]
et :
\[
\frac 37 \in ]-1;1[ \implies \lim_{n\to+\infty} \left(\frac37\right)^n = 0.
\]
En sommant ces deux limites, on obtient que :
\[\lim_{n\to+\infty} -\left(\frac97\right)^n + \left(\frac37\right)^n = -\infty.\]
La suite $(u_n)$ est donc majorée par une suite tendant vers $-\infty$. Elle tend donc elle-même vers cette limite.
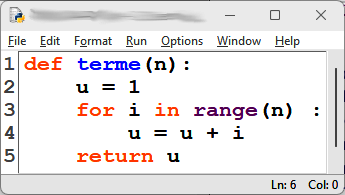
On considère la fonction suivante écrite en langage Python :
Corrigé
Affirmation vraie.
Lors de l'appel de terme(4), la valeur de n est 4. Donc la boucle "for i in range(n)" tournera quatre fois, pour les valeurs de i allant de 0 à 3.
Au départ u vaut 1.
Lors du premier tour de boucle (quand i = 0), u prend la valeur 1+0, donc u vaut encore 1.
Lors du deuxième tour de boucle (quand i = 1), u prend la valeur 1+1, donc u prend la valeur 2.
Lors du troisième tour de boucle (quand i =2), u prend la valeur 2+2, donc u prend la valeur 4.
Lors du quatrième tour de boucle (quand i =3), u prend la valeur 4+3, donc u prend la valeur 7.
On sort alors de la boucle et on retourne u, donc on retourne bien la valeur 7.
Au départ u vaut 1.
Lors du premier tour de boucle (quand i = 0), u prend la valeur 1+0, donc u vaut encore 1.
Lors du deuxième tour de boucle (quand i = 1), u prend la valeur 1+1, donc u prend la valeur 2.
Lors du troisième tour de boucle (quand i =2), u prend la valeur 2+2, donc u prend la valeur 4.
Lors du quatrième tour de boucle (quand i =3), u prend la valeur 4+3, donc u prend la valeur 7.
On sort alors de la boucle et on retourne u, donc on retourne bien la valeur 7.
Lors d'un concours, le gagnant a le choix entre deux prix :
- Prix A : il reçoit 1000 euros par jour pendant 15 jours;
- Prix B : il reçoit 1 euro le 1er jour, 2 euros le 2e jour, 4 euros le 3e jour et pendant 15 jours la somme reçue double chaque jour.
Corrigé
Affirmation fausse. Le prix A vaut $15\times 1000 = 15000$ €.
Le prix B vaut \[\begin{aligned} 1+2+2^2 + 2^3 + \cdot + 2^{14} &= \frac{1-2^{15}}{1-2}& \\ &= \frac{1-32768}{-1}& \\ &= 32767\:\text{€}& \end{aligned}\] Le prix B est plus de deux fois supérieur au prix A !
Le prix B vaut \[\begin{aligned} 1+2+2^2 + 2^3 + \cdot + 2^{14} &= \frac{1-2^{15}}{1-2}& \\ &= \frac{1-32768}{-1}& \\ &= 32767\:\text{€}& \end{aligned}\] Le prix B est plus de deux fois supérieur au prix A !
On considère la suite $\left(v_n\right)$ définie pour tout entier $n \ge 1$ par \[v_n = \displaystyle\int_1^n \ln x\:\text{d}x.\] Affirmation 5 : La suite $\left(v_n\right)$ est croissante.
Corrigé
Affirmation vraie.
➔Premier argument. Sur $[1;+\infty[$ la fonction $\ln$ est positive et $n\ge 1$. Donc l'intégrale proposée représente l'aire sous la courbe de $y=\ln(x)$, entre les droites d'équation $x=1$ et $x=n$.
Donc plus $n$ est grand, plus $v_n$ est grande. La suite $(v_n)$ est croissante.
➔Deuxième argument. À l'aide de la relation de Chasles, on peut écrire que pour tout entier naturel $n$: \[\begin{aligned} v_{n+1} - v_n &= \int_1^{n+1} \ln(x)\:\mathrm dx - \int_1^n \ln(x)\:\mathrm dx& \\ &=\int_1^{n} \ln(x)\:\mathrm dx + \int_n^{n+1}\ln(x)\:\mathrm dx - \int_1^n\ln(x)\:\mathrm dx& \\ &=\int_n^{n+1}\ln(x)\:\mathrm dx.& \end{aligned}\] Puisque $n$ et $n+1$ appartiennent à $[1;+\infty[$ et que la fonction $\ln$ est positive sur $[1;+\infty[$, alors \[\int_n^{n+1}\ln(x)\:\mathrm dx \ge 0 \implies v_{n+1} - v_n \ge 0.\] Ce qui prouve que $(v_n)$ est une suite croissante.
➔Troisième argument. La fonction $F$ définie sur $[1;+\infty[$ par \[F(x) = \int_1^n \ln(x)\mathrm dx\] est la primitive de $x\mapsto \ln(x)$ sur $[1;+\infty[$ qui s'annule en 1.
Or $\ln$ est positive sur $[1;+\infty[$, donc $F$ est croissante. Donc pour tout entier naturel $n>0$: \[F(n+1) \ge F(n) \implies v_{n+1} \ge v_n.\] Ce qui montre aussi la croissance de la suite $(v_n)$.
➔Premier argument. Sur $[1;+\infty[$ la fonction $\ln$ est positive et $n\ge 1$. Donc l'intégrale proposée représente l'aire sous la courbe de $y=\ln(x)$, entre les droites d'équation $x=1$ et $x=n$.
Donc plus $n$ est grand, plus $v_n$ est grande. La suite $(v_n)$ est croissante.
➔Deuxième argument. À l'aide de la relation de Chasles, on peut écrire que pour tout entier naturel $n$: \[\begin{aligned} v_{n+1} - v_n &= \int_1^{n+1} \ln(x)\:\mathrm dx - \int_1^n \ln(x)\:\mathrm dx& \\ &=\int_1^{n} \ln(x)\:\mathrm dx + \int_n^{n+1}\ln(x)\:\mathrm dx - \int_1^n\ln(x)\:\mathrm dx& \\ &=\int_n^{n+1}\ln(x)\:\mathrm dx.& \end{aligned}\] Puisque $n$ et $n+1$ appartiennent à $[1;+\infty[$ et que la fonction $\ln$ est positive sur $[1;+\infty[$, alors \[\int_n^{n+1}\ln(x)\:\mathrm dx \ge 0 \implies v_{n+1} - v_n \ge 0.\] Ce qui prouve que $(v_n)$ est une suite croissante.
➔Troisième argument. La fonction $F$ définie sur $[1;+\infty[$ par \[F(x) = \int_1^n \ln(x)\mathrm dx\] est la primitive de $x\mapsto \ln(x)$ sur $[1;+\infty[$ qui s'annule en 1.
Or $\ln$ est positive sur $[1;+\infty[$, donc $F$ est croissante. Donc pour tout entier naturel $n>0$: \[F(n+1) \ge F(n) \implies v_{n+1} \ge v_n.\] Ce qui montre aussi la croissance de la suite $(v_n)$.
retour
code : 888