AP06a/02
retour

Une chaîne de salles de sport propose trois formules d'abonnement mensuel :
- Formule A : accès aux cours collectifs;
- Formule B : accès libre à la salle de musculation;
- Formule C : accès libre à la salle de musculation et aux cours collectifs.
On a observé que :
- 43 % des clients de cette chaîne sont des hommes;
- 13 % des hommes et 62 % des femmes ont choisi la formule A;
- 74 % des hommes et 20 % des femmes ont choisi la formule B;
- Les autres ont choisi la formule C.
On choisit au hasard la fiche d'un client. On considère les évènements suivants :
- $F$ : « le client est une femme »;
- $H$ : « le client est un homme »;
- $A$ : « le client a choisi la formule A »;
- $B$ : « le client a choisi la formule B »;
- $C$ : « le client a choisi la formule C ».
1. Recopier et compléter l'arbre de probabilités ci-dessous :
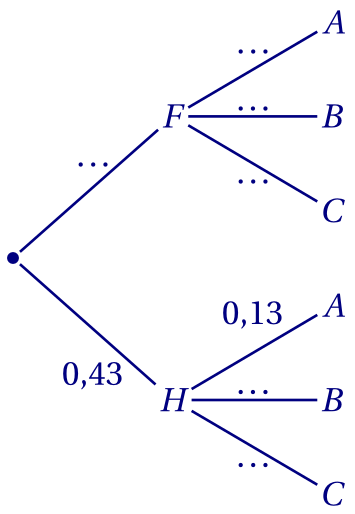
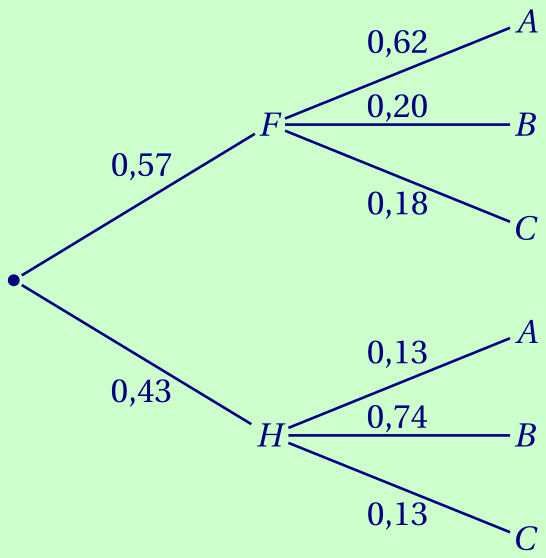
Corrigé

2.a. Définir par une phrase l'évènement $H \cap A$.
Corrigé
$H\cap A$ est l'événement «le client est un homme qui a choisi la formule A».
2.b. Calculer la probabilité $P(H \cap A)$. En donner la valeur exacte.
Corrigé
$P(H\cap A) = P(H)\times P_H(A) = 0,43 \times 0,13 = 0,0559$.
3. Montrer que $P(A) = 0,4093$.
Corrigé
$P(A) = P(A\cap H) + P(A\cap F)$
$= P(A\cap H) + P(F)\times P_F(A)$
$=0,0559 + 0,57 \times 0,62$
$=0,0559 + 0,3534$
$=0,4093.$
$= P(A\cap H) + P(F)\times P_F(A)$
$=0,0559 + 0,57 \times 0,62$
$=0,0559 + 0,3534$
$=0,4093.$
4.
Le client a choisi la formule A. Calculer la probabilité que ce soit un homme.
Le résultat sera arrondi à 10−4.
Corrigé
On cherche $P_A(H)$. Par définition:
$P_A(H) = \dfrac{P(A\cap H)}{P(A)} = \dfrac{0,0559}{0,4093} \approx 0,1366$.
$P_A(H) = \dfrac{P(A\cap H)}{P(A)} = \dfrac{0,0559}{0,4093} \approx 0,1366$.
retour
code : 876