875
retour
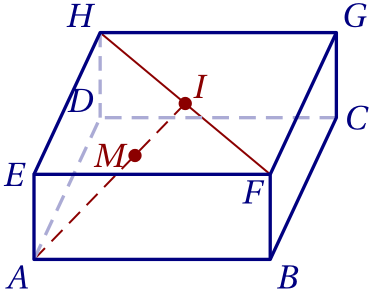
$ABCDEFGH$ est le parallélépipède rectangle représenté ci-contre.
$I$ est le milieu de $[HF]$ et $M$ est le point défini par la relation $3\overrightarrow{AM}=2\overrightarrow{AI}$.
Démontrer que les points $E$, $C$ et $M$ sont alignés.
Corrigé
Plaçons nous dans le repère $(A;\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AE})$.
Dans ce repère, $E$ a pour coordonnées $(0;0;1)$, $C$ a pour coordonnées $(1;1;0)$, $H$ a pour coordonnées $(0;1;1)$ et $F$ a pour coordonnées $(1;0;1)$.
Donc le milieu $I$ de $[FH]$ a pour coordonnées \[\left(\frac{1+0}2;\frac{0+1}2;\frac{1+1}2\right) = \left(\frac 12;\frac 12; 1\right).\] Le point $M$ vérifie la relation : \[3\overrightarrow{AM} = 2\overrightarrow{AI} \iff \overrightarrow{AM} = \frac 23\overrightarrow{AI}.\] Donc les coordonnées du point $M$ (qui sont aussi celles du vecteur $\overrightarrow{AM}$) sont calculées par : \[\frac 2 3 \times \left( \frac 1 2; \frac 12 ; \frac 12\right) = \left(\frac 13 ; \frac 13 ; \frac 23\right).\] Le vecteur $\overrightarrow{EC}$ a pour coordonnées : \[\begin{pmatrix}1-0\\1-0\\0-1\end{pmatrix} = \begin{pmatrix}1\\1\\-1\end{pmatrix}.\] Le vecteur $\overrightarrow{EM}$ a pour coordonnées : \[\begin{pmatrix}\frac 13 - 0 \\ \frac13 - 0 \\ \frac 23 - 1\end{pmatrix} = \begin{pmatrix}\frac13 \\ \frac13 \\ -\frac13\end{pmatrix}.\] On remarque que : \[\begin{pmatrix}\frac13 \\ \frac13 \\ -\frac13\end{pmatrix} = \frac 1 3 \times \begin{pmatrix}1\\1\\-1\end{pmatrix} \implies \overrightarrow{EM} = \frac 13\overrightarrow{EC}.\] Les vecteurs $\overrightarrow{EM}$ et $\overrightarrow{EC}$ étant colinéaires, les points $E$, $M$ et $C$ sont alignés.
Dans ce repère, $E$ a pour coordonnées $(0;0;1)$, $C$ a pour coordonnées $(1;1;0)$, $H$ a pour coordonnées $(0;1;1)$ et $F$ a pour coordonnées $(1;0;1)$.
Donc le milieu $I$ de $[FH]$ a pour coordonnées \[\left(\frac{1+0}2;\frac{0+1}2;\frac{1+1}2\right) = \left(\frac 12;\frac 12; 1\right).\] Le point $M$ vérifie la relation : \[3\overrightarrow{AM} = 2\overrightarrow{AI} \iff \overrightarrow{AM} = \frac 23\overrightarrow{AI}.\] Donc les coordonnées du point $M$ (qui sont aussi celles du vecteur $\overrightarrow{AM}$) sont calculées par : \[\frac 2 3 \times \left( \frac 1 2; \frac 12 ; \frac 12\right) = \left(\frac 13 ; \frac 13 ; \frac 23\right).\] Le vecteur $\overrightarrow{EC}$ a pour coordonnées : \[\begin{pmatrix}1-0\\1-0\\0-1\end{pmatrix} = \begin{pmatrix}1\\1\\-1\end{pmatrix}.\] Le vecteur $\overrightarrow{EM}$ a pour coordonnées : \[\begin{pmatrix}\frac 13 - 0 \\ \frac13 - 0 \\ \frac 23 - 1\end{pmatrix} = \begin{pmatrix}\frac13 \\ \frac13 \\ -\frac13\end{pmatrix}.\] On remarque que : \[\begin{pmatrix}\frac13 \\ \frac13 \\ -\frac13\end{pmatrix} = \frac 1 3 \times \begin{pmatrix}1\\1\\-1\end{pmatrix} \implies \overrightarrow{EM} = \frac 13\overrightarrow{EC}.\] Les vecteurs $\overrightarrow{EM}$ et $\overrightarrow{EC}$ étant colinéaires, les points $E$, $M$ et $C$ sont alignés.
retour
code : 875