874

retour

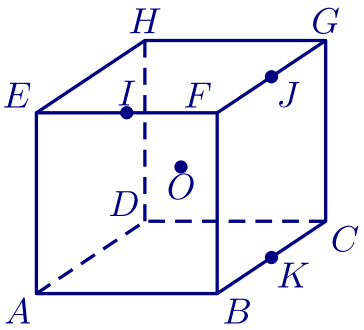
Soit $ABCDEFGH$ le cube représenté ci-contre.

$I$, $J$ et $K$ sont les milieux respectifs des arêtes $[EF]$, $[FG]$ et $[BC]$.

$O$ est le centre de ce cube.

1. En utilisant les points de la figure, citer un vecteur égal à

a. $\overrightarrow{DC}$; Corrigé

$\overrightarrow{AB}$, $\overrightarrow{EF}$, $\overrightarrow{HG}$.

b. $\overrightarrow{GJ}$; Corrigé

$\overrightarrow{JF}$, $\overrightarrow{CK}$, $\overrightarrow{KB}$.

c. $\overrightarrow{JK}$; Corrigé

$\overrightarrow{EA}$, $\overrightarrow{FB}$, $\overrightarrow{GC}$, $\overrightarrow{HD}$.

d. $\overrightarrow{IF}$. Corrigé

$\overrightarrow{EI}$.

2. Recopier ces relations vectorielles en remplaçant les pointillés par un sommet de la figure.

a. $\overrightarrow{HG} +\overrightarrow{\ldots J} = \overrightarrow{HJ}$. Corrigé

$\overrightarrow{HG} +\overrightarrow{\mathbf{G}J} = \overrightarrow{HJ}$.

b. $\overrightarrow{H\ldots} = \dfrac 1 2 \overrightarrow{HB}$. Corrigé

$\overrightarrow{H\mathbf{O}} = \dfrac 1 2 \overrightarrow{HB}$.

c. $\overrightarrow{EB} = 2\overrightarrow{O\ldots}$. Corrigé

$\overrightarrow{EB} = 2\overrightarrow{O\mathbf{K}}$.

d. $\overrightarrow{EB}+\overrightarrow{\ldots J} = \overrightarrow{AK}$. Corrigé

$\overrightarrow{EB}+\overrightarrow{\mathbf{B}J} = \overrightarrow{AK}$.

retour

code : 874