EX-02
retour
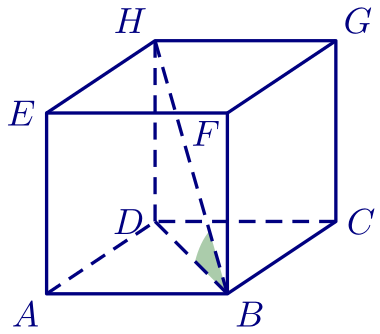
$ABCDEFGH$ est un cube de côté 5.
1. Calculer la longueur $DB$.
Corrigé
Puisque la face $ABCD$ est un carré, le triangle $ABD$ est rectangle en $A$ et selon
le théorème de Pythagore.
\[\begin{aligned}
&DB^2 = DA^2 + AB^2 = 5^2 + 5^2 = 50&
\\
\implies
&BD = \sqrt{50} = \sqrt{25\times 2} = 5\sqrt 2.&
\end{aligned}\]
2. En déduire la mesure en degrés de l'angle $\widehat{DBH}$, arrondie à l'unité.
Corrigé
L'arête $[HD]$ étant perpendiculaire à la face $ABCD$, le triangle $BDH$ est rectangle en $D$.
Donc : \[\tan\widehat{DBH} = \frac{DH}{DB} = \frac{5}{5\sqrt 2} = \frac 1 {\sqrt 2}.\] Par conséquent : \[\widehat{DBH} = \arctan\left(\frac 1{\sqrt 2}\right) \approx 35\text{°}.\]
Donc : \[\tan\widehat{DBH} = \frac{DH}{DB} = \frac{5}{5\sqrt 2} = \frac 1 {\sqrt 2}.\] Par conséquent : \[\widehat{DBH} = \arctan\left(\frac 1{\sqrt 2}\right) \approx 35\text{°}.\]
retour
code : 873