Pour tout réel $x$, $\mathrm e^x$ est strictement positif; sachant que $x$ est supérieur à $-1$, $x+1$ est lui aussi strictement positif.
Le produit de ces deux facteurs est donc strictement positif. \[\begin{array}{|l|lcr|} \hline x &-1&\qquad\qquad&+\infty \\ \hline f(x) &&+& \\ \hline \end{array}\]

$f=\frac u v$ où $u$ et $v$ sont définies sur $]-1;+\infty[$ par \[u(x) = \mathrm e^x \quad\text{et}\quad v(x) = x + 1.\] $u$ est dérivable sur $]-1;+\infty[$ et $v$ est dérivable et non nulle sur $]-1;+\infty[$. Donc $f$ est aussi dérivable sur $]-1;+\infty[$ avec \[f' = \frac{u'v - uv'}{v^2}.\] Sachant que \[u'(x) = \mathrm e^x \quad\text{et}\quad v'(x) = 1,\] pour tout réel $x\ge -1$: \[\begin{aligned} f'(x) &= \frac{\mathrm e^x\cdot(x+1) - \mathrm e^x \cdot 1}{(x+1)^2}& \\ &=\frac{x\mathrm e^x + \mathrm e^x - \mathrm e^x}{(x+1)^2}& \\ &=\frac{x\mathrm e^x}{(x+1)^2}.& \end{aligned}\] Les facteurs $\mathrm e^x$ et $(x+1)^2$ étant strictement positifs, $f'(x)$ est du même signe que $x$. D'où le tableau de variation suivant (les éléments en rouge ne sont exigibles qu'en terminale). 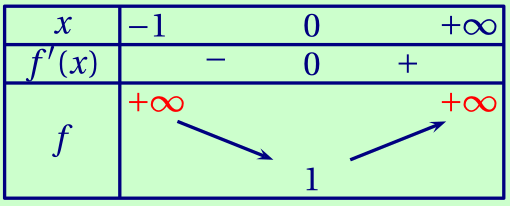Avec : \[f(0) = \frac{\mathrm e^0}{0+1} = \frac 1 1 = 1.\] (Terminale seulement.) \[\lim_{\substack{x\to-1\\x\ge-1}} x + 1 = 0^+\] et \[\lim_{x\to-1}\mathrm e^x = \mathrm e^{-1}\quad\text{avec}\quad \mathrm e^{-1}>0.\] Donc \[\lim_{\substack{x\to-1\\x\ge-1}} \frac{\mathrm e^{x}}{x-1} = +\infty.\] D'autre part, pour $x\neq 0$: \[\frac{\mathrm e^x}{x+1} = \frac{x\left(\frac{\mathrm e^x}x \right)}{x\left(1+\frac 1 x \right)} =\frac{\frac{\mathrm e^x}x}{1+\frac 1 x}.\] Nous savons (cours sur les croissances comparées) que \[\lim_{x\to+\infty} \frac{\mathrm e^x} x = +\infty\] et que \[\lim_{x\to+\infty} \frac 1 x = 0 \implies \lim_{x\to+\infty} 1+\frac 1 x = 1.\] Donc: \[\lim_{x\to+\infty} \frac{\frac{\mathrm e^x}x}{1+\frac 1 x} = +\infty.\]