EX-
retour
Les rues d'une ville nouvelle sont structurées de telle sorte que les pâtés de maisons sont des carrés superposables et les rues sont toutes parallèles ou perpendiculaires.
On identifie le plan de la ville au quadrillage d'un carré de 10 unités sur 10 dans lequel on se repère avec des points à coordonnées entières qui correspondent aux carrefours :
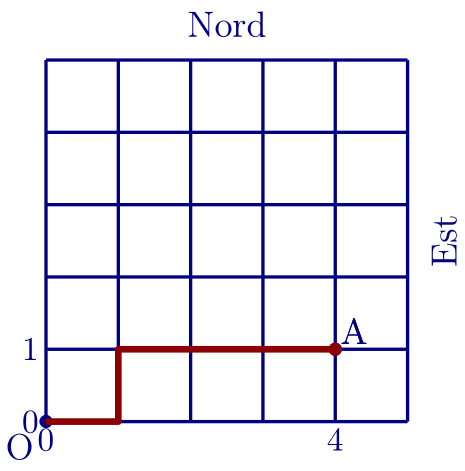
Le point O a pour coordonnées (0;0), le point A a pour coordonnées (4;1).
un promeneur part de O et à chaque intersection la probabilité qu'il aille vers le Nord est de $\dfrac{2}{3}$ (et donc de $\dfrac{1}{3}$ vers l'Est), indépendamment de son choix précédent. Il ne se dirige jamais vers le Sud ou l'Ouest.
Dans tout l'exercice, on décrit son chemin à l'aide d'un mot composé successivement des lettres N ou E qui indiquent dans l'ordre la direction à suivre à chaque intersection.
On appelle longueur d'un chemin le nombre de lettres employées pour le décrire.
Par exemple : pour se rendre en A, il peut suivre le chemin ENEEE (marqué en rouge sur la figure); Ce chemin a une longueur égale à 5.
On ne s'intéresse dans la suite qu'aux chemins de longueur 5 partant de O.
On appelle $X$ la variable aléatoire qui à tout chemin suivi par le promeneur associe le nombre de fois où il va vers le Nord.
1.
Énumérer, en donnant la liste de leurs coordonnées, tous les points sur lesquels
peut aboutir un chemin.
Corrigé
2.
Justifier que $X$ suit une loi binomiale dont on donnera les paramètres.
Corrigé
Cette expérience est répétée cinq fois de manière indépendante.
Donc $X$ suit la loi binomiale de paramètres $n= 5$ et $p=\dfrac 1 2$.
3.
Calculer la probabilité que le promeneur arrive en A.
Corrigé
C'est donc aussi l'événement $\{X=1\}$.
Alors \[P(X=1) = \binom{5}{1} \times \left(\frac 1 2\right)^1 \times \left(\frac 1 2\right)^4 = \frac 5 {32}.\]
retour
code : 854