EX-22

retour

Un berger dispose d'un champ situé devant sa bergerie. Il décide de poser une clôture pour obtenir un enclos rectangulaire dont l'un des côtés sera le mur de la bergerie selon le plan ci-dessous.

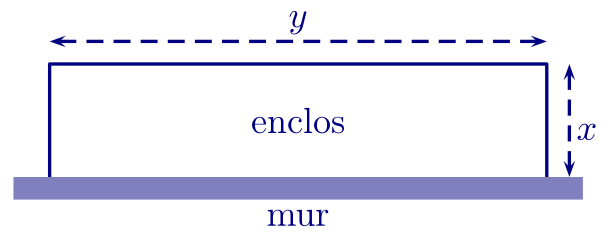
Ce champ doit avoir une aire de 300 m².

Le but de cet exercice est de trouver les dimensions $x$ et $y$ du champ pour que la longueur de la clôture soit minimale.

1. Sachant que l'aire du champ est égale à \np[m^2]{300}, exprimer $y$ en fonction de $x$ .
Corrigé

Puisque le rectangle à une aire de 300 m²:

x y = 300 ⟺ y = \frac{300}{x} .

2. Exprimer en fonction de $x$ la longueur de la clôture, en m, notée $ℓ (x)$ .
Corrigé

Longueur de la clôture :

ℓ (x) = 2 x + y = 2 x + \frac{300}{x} .

3. Calculer la dérivée $ℓ^{'}$ de $ℓ$ .
Corrigé

ℓ

est dérivable sur

] 0; + \infty [

ℓ^{'} (x) = 2 - 300 \times (- \frac{1}{x^{2}}) = 2 - \frac{300}{x^{2}} = \frac{2 x^{2} - 300}{x^{2}} .

4. Étudier les variations de $ℓ$ sur $] 0; + \infty [$ .
Corrigé

Puisque le dénominateur

x^{2}

est strictement positif,

ℓ^{'} (x)

a le même signe que le polynôme de degré 2

2 x^{2} - 300

.
Ce polynôme s'annule quand

\begin{aligned} 2 x^{2} - 300 & = 0 \\ ⟺ x^{2} & = \frac{300}{2} = 150 \\ ⟺ x & = \pm \sqrt{150} = \pm 5 \sqrt{6} . \end{aligned}

Son coefficient de degré 2 est positif donc il est positif à l'extérieur de ses racines :

\begin{array}{cccccccc} x & - \infty & - 5 \sqrt{6} & 5 \sqrt{6} & + \infty \\ x^{2} - 300 & + & 0 & - & 0 & + \end{array}

Donc on obtient le tableau de variation suivant.

\begin{array}{cccccc} x & 0 & 5 \sqrt{6} & + \infty \\ ℓ^{'} & - & 0 & + \\ ℓ (x) & ↘ & ↗ \\ 20 \sqrt{6} \end{array}

Avec :

\begin{aligned} ℓ (5 \sqrt{6}) & = 2 \times 5 \sqrt{6} + \frac{300}{5 \sqrt{6}} \\ = 10 \sqrt{6} + \frac{60}{\sqrt{6}} \\ = 10 \sqrt{6} + \frac{60 \sqrt{6}}{(\sqrt{6})^{2}} \\ = 10 \sqrt{6} + \frac{60 \sqrt{6}}{6} \\ = 10 \sqrt{6} + 10 \sqrt{6} \\ = 20 \sqrt{6} . \end{aligned}

5. En déduire les dimensions $x$ et $y$ pour lesquelles la clôture a une longueur minimale.
Préciser cette longueur.
Corrigé

D'après le tableau de variation établi à la question précédente,

ℓ

admet son minimum en

5 \sqrt{6}

qui vaut

20 \sqrt{6}

.
La plus petite clôture a donc pour dimensions (en mètres)

x = 5 \sqrt{6} ⟹ y = \frac{300}{5 \sqrt{6}} = \frac{60}{\sqrt{6}} = \frac{60 \sqrt{6}}{6} = 60 \sqrt{6} .

Elle mesure alors

20 \sqrt{6}

mètres.

retour

code : 841