7.03 (d'après bac 2023)

retour

Partie A

On considère la fonction $g$ définie sur l'intervalle $]0;+\infty[$ par \[g(x) = \ln \left(x^2\right) + x - 2\]

1. Déterminer les limites de la fonction $g$ aux bornes de son ensemble de définition.
Corrigé

Puisque $\displaystyle\lim_{x\to0} x^2 = 0$, $\displaystyle\lim_{x\to0} \ln(x^2) = -\infty$. D'autre part $\displaystyle\lim_{x\to0} x = 0$, donc en sommant ces limites $\displaystyle\lim_{x\to0} \ln(x)^2 + x - 2 = -\infty$.
Puisque $\displaystyle\lim_{x\to+\infty} x^2 = +\infty$, $\displaystyle\lim_{x\to+\infty}\ln(x^2) = +\infty$. D'autre part $\displaystyle\lim_{x\to+\infty} x = +\infty$ donc en sommant ces limites $\displaystyle\lim_{x\to+\infty} \ln(x^2) + x - 2 = +\infty$.

2. On admet que la fonction $g$ est dérivable sur l'intervalle $]0;+\infty[$.
Étudier les variations de la fonction $g$ sur l'intervalle $]0;+\infty[$.
Corrigé

Pour tout réel $x>0$: \[g'(x) = \dfrac{2x}{x^2} + 1 - 0 = \frac 2 x + 1.\] Or \[x > 0 \implies \frac 2 x > 0 \implies \frac 2 x + 1 > 1 \implies g'(x) > 0.\] La fonction $g$ est donc strictement croissante sur $]0;+\infty[$.

3.a. Démontrer qu'il existe un unique réel strictement positif $\alpha$ tel que $g(\alpha) = 0$.
Corrigé

La fonction $g$ est continue sur $]0;+\infty[$, avec $\displaystyle\lim_{x\to0} g(x) = -\infty$ et $\displaystyle\lim_{x\to+\infty} g(x) = +\infty$. De plus, $g$ est strictement croissante.
Donc, selon le corollaire du théorème des valeurs intermédiaires, tout réel $y$ est l'image d'un unique réel $x\in]0;+\infty[$ par $g$.
C'est le cas en particulier de $y = 0$ qui admet donc un unique antécédent $\alpha$ par $g$.

b. Déterminer un encadrement de $\alpha$ d'amplitude $10^{-2}$.
Corrigé

Une recherche à l'aide de la calculatrice permet d'établir que \begin{align*} g(1,37) &\approx -0,00038& \implies g(1,37) &< 0 \\ g(1,38) &\approx 0,02417& \implies g(1,38) &> 0 \end{align*} Donc $\alpha \in ]1,37\;;\;1,38[$.

4. En déduire le tableau de signe de la fonction $g$ sur l'intervalle $]0;+\infty[$.
Corrigé

La fonction $g$ étant strictement croissante: \begin{align*} &x_1 < \alpha < x_2& \\ \implies &g(x_1) < g(\alpha) < g(x_2)& \\ \implies &g(x_1) < 0 < g(x_2).& \end{align*} On peut donc établir le tableau de signe suivant \[\begin{array}{l|llcrr} x &0&\qquad\qquad&\alpha&\qquad\qquad&+\infty \\ \hline g(x) &&-&0&+&\\ \end{array}\]

Partie B

On considère la fonction $f$ définie sur l'intervalle $]0;+\infty[$ par : \[f(x) = \dfrac{(x-2)}{x}\ln(x).\] On note $\mathcal{C}_f$ sa courbe représentative dans un repère orthonormé.

1.a. Déterminer la limite de la fonction $f$ en 0.
Corrigé

Sachant que $\displaystyle\lim_{x\to 0} x- 2 = -2$ et $\displaystyle\lim_{x\to0^+} x = 0^+$, le quotient vérifie $\displaystyle\lim_{x\to0} \frac{x-2}x = -\infty$.
D'autre part, $\displaystyle\lim_{x\to0} \ln(x) = -\infty$, donc en réalisant le produit de ces limites $\displaystyle\lim_{x\to0} \frac{x-2}{x}\ln(x) = +\infty$.

b. Interpréter graphiquement le résultat.
Corrigé

On en déduit que la droite d'équation $x=0$ (l'axe des ordonnées) est une asymptote verticale à $\mathcal C_f$.

2. Déterminer la limite de la fonction $f$ en $+\infty$.
Corrigé

Pour tout $x\in]0;+\infty[$: \begin{align*} f(x) &= \dfrac{(x-2)}{x}\ln(x)& \\ &= \left(\dfrac x x - \dfrac 2 x\right)\ln(x)& \\ &= \left(1-\dfrac 2 x\right)\ln(x).& \end{align*} $\displaystyle\lim_{x\to+\infty} \dfrac 2 x = 0$ donc $\displaystyle\lim_{x\to+\infty} 1 - \dfrac x 2 = 1$.
D'autre part $\displaystyle\lim_{x\to+\infty}\ln(x) = +\infty$ , donc par produit de limites $\displaystyle\lim_{x\to+\infty} \left(1-\dfrac 2 x\right)\ln(x) = +\infty$.

3. On admet que la fonction $f$ est dérivable sur l'intervalle $]0;+\infty[$.
Montrer que pour tout réel $x$ strictement positif, on a \[f'(x)=\dfrac{g(x)}{x^2}.\] Corrigé

On a montré précédemment que pour tout $x\in]0;+\infty[$: \[f(x) = \left(1-\frac 2 x\right)\ln(x).\] Alors : \begin{align*} g'(x)&=\left(0-2\times \left(-\frac 1 {x^2}\right)\right)\ln(x) + \left(1 - \frac 2 x\right)\cdot\frac 1 x& \\ &=\frac{2\ln(x)}{x^2} + \frac 1 x - \frac 2 {x^2}& \\ &=\frac{2\ln(x)}{x^2} + \frac x {x^2} - \frac 2 {x^2}& \\ &=\frac{2\ln(x) + x -2}{x^2}& \\ &=\frac{\ln(x^2) +x - 2}{x^2}& \\ &=\frac{g(x)}{x^2}.& \end{align*}

4. En déduire les variations de la fonction $f$ sur l'intervalle $]0;+\infty[$.
Corrigé

Puisque $x^2 >0$, le signe de $f'(x)$ est celui de $g(x)$, qui a été établi à la question A-4.
Sur $]0;\alpha[$, $f'$ est strictement négative puis sur $]\alpha;+\infty[$, $f'$ est strictement positive.
La fonction $f$ est donc strictement décroissante sur $]0;\alpha]$ puis strictement croissante sur $[\alpha;+\infty[$.

Partie C

Étudier la position relative de la courbe $\mathcal{C}_f$ et de la courbe représentative de la fonction $\ln$ sur l'intervalle $]0;+\infty[$.
Corrigé

Pour tout réel $x>0$: \begin{align*} f(x) - \ln(x) &= \frac{x-2}x\ln(x) - \ln(x)& \\ &=\left(\frac{x-2}x - 1\right)\ln(x)& \\ &=\left(\frac{x-2-x}x\right)\ln(x)& \\ &=-\frac 2 x\ln(x).& \end{align*} Puisque $x > 0$, le facteur $-\dfrac 2 x$ est strictement négatif, donc $f(x)-\ln(x)$ a le signe opposé de celui de $\ln(x)$.
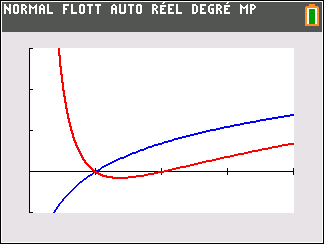
Pour $x\in ]0;1[$, $f(x)-\ln(x)$ est positive, donc $\mathcal C_f$ est au dessus de la courbe de $x\mapsto \ln(x)$.
Si $x= 1$, $f(x) - \ln(x) = 0$ donc les deux courbes se coupent au point d'abscisse 1.
Si $x\in ]1;+\infty[$, $f(x) - \ln(x) < 0$ donc $\mathcal C_f$ est au dessous de la courbe de $x\mapsto \ln(x)$.

On peut vérifier cette réponse à l'aide de la calculatrice graphique.

retour

code : 815