retour

Partie A

On considère la suite $\left(u_n\right)_{n\in \mathbb N}$ définie par $u_0 = 400$ et pour tout entier naturel $n$: \[u_{n+1} = 0,9u_n + 60.\]

1. 1. Calculer $u_1$ et $u_2$.
      Corrigé
      $u_1 = 0,9u_0 + 60 = 0,9\times 400 + 60 = 420$;
      $u_2 = 0,9u_1 + 60 = 0,9\times 420 + 60 = 438$.
   2. Conjecturer le sens de variation de la suite $\left(u_n\right)_{n\in \mathbb N}$
      Corrigé
      Puisque $u_0 < u_1 < u_2$, on peut conjecturer que la suite $(u_n)$ serait croissante.
2. Montrer, par récurrence, que pour tout entier naturel $n$, on a l'inégalité \[0 \leqslant u_n \leqslant u_{n+1} \leqslant 600.\] Corrigé
   Notons $\mathcal P(n)$ l'assertion :
   «$0\leqslant u_n \leqslant u_{n+1} \leqslant 600$».
   Puisque $u_0 = 400$ et $u_1 = 438$, on a bien $0 \leqslant u_0 \leqslant u_1 \leqslant 600$. $\mathcal P(0)$ est donc vraie (initialisation).
   Supposons que pour un rang $n$ donné quelconque, $\mathcal P(n)$ soit vraie. Alors \[\begin{aligned} 0 &\leqslant u_n \leqslant u_{n+1}& \\ \implies 0,9\times 0 &\leqslant 0,9u_n \leqslant 0,9u_{n+1}& \\ \implies 0 + 60 &\leqslant 0,9u_n + 60 \leqslant 0,9u_{n+1}+60& \\ \implies 60 &\leqslant u_{n+1} \leqslant u_{n+2}& \end{aligned}\] Puisque $60 > 0$, on a donc bien a fortiori \[0 \leqslant u_{n+1} \leqslant u_{n+2}.\] Donc si $\mathcal P(n)$ est vraie, alors $\mathcal P(n+1)$ le sera aussi (hérédité).
   Par récurrence, pour tout entier naturel $n$, $\mathcal P(n)$ est vraie.
3. 1. Montrer que la suite $\left(u_n\right)_{n\in \mathbb N}$ est convergente.
      Indication Corrigé
      Quels propriétés de la suite $(u_n)$ a-t-on démontré à la question précédente?
      On vient de montrer que la suite $(u_n)_{n\in\mathbb N}$ est croissante et majorée par 600.
      Elle converge donc vers un réel inférieur ou égal à 600.
   2. Déterminer la limite de la suite $\left(u_n\right)_{n\in \mathbb N}$. Justifier.
      Indication Corrigé
      Si $f$ est la fonction continue telle que \[u_{n+1} = f(u_n)\] et si la suite $(u_n)$ converge vers $\ell$, alors \[f(\ell) = \ell.\]
      La fonction $f: x\mapsto 0,9x + 60$ est affine, donc continue sur $\mathbb R$ et pour tout entier naturel $n$, $u_{n+1} = f(u_n)$.
      La limite $\ell$ de la suite $(u_n)$ vérifie donc \[\begin{aligned} \ell &= f(\ell)& \\ \iff \ell &= 0,9\ell + 60& \\ \iff \ell - 0,9\ell &= 60& \\ \iff 0,1\ell &= 60& \\ \iff \ell &= \frac{60}{0,1}& \\ \iff \ell &=600.& \end{aligned}\] La suite $(u_n)_{n\in\mathbb N}$ converge donc vers 600.
4. On donne une fonction écrite en langage Python:
   def mystere(seuil): n=0 u=400 while u <= seuil: n = n+1 u = 0.9*u+60 return n
   Quelle valeur obtient-on en tapant dans la console de Python: mystere(500)?
   Corrigé
   La fonction mystere calcule les termes successifs de la suite $(u_n)_{n\in\mathbb N}$ tant que ces termes restent inférieur ou égaux au seuil.
   Elle retourne donc le rang du premier terme de la suite qui dépasse seuil.
   Cherchons donc, de manière heuristique, le premier terme de la suite qui dépasse 500.
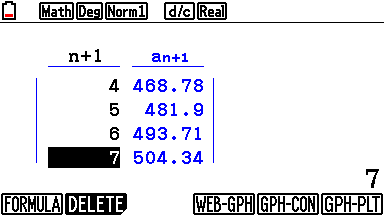
   D'après la calculatrice : \[\begin{aligned} u_6 \approx 493,71 &\implies u_6 < 500\;;& \\ u_7 \approx 504,35 &\implies u_7 > 500.& \end{aligned}\] La valeur obtenue sera donc : 7.

   

Partie B

Un arboriculteur possède un verger dans lequel il a la place de cultiver au maximum 500 arbres.
Chaque année il vend 10 % des arbres de son verger et puis il replante 60 nouveaux arbres.
Le verger compte 400 arbres en 2023.
L'arboriculteur pense qu'il pourra continuer à vendre et à planter les arbres au même rythme pendant les années à venir.
Va-t-il être confronté à un problème de place dans son verger ? Expliquer votre réponse.

Indication Corrigé

retour

code : 803