EX-
retour
Dans tout cet exercice, les probabilités seront arrondies, si nécessaire, à 10−3.
D'après une étude, les utilisateurs réguliers de transports en commun représentent 17 % de la population française.
Parmi ces utilisateurs réguliers, 32 % sont des jeunes âgés de 18 à 24 ans. (Source : TNS-Sofres)
Partie A :
On interroge une personne au hasard et on note :
- R l'évènement : "La personne interrogée utilise régulièrement les transports en commun".
- J l'évènement : "La personne interrogée est âgée de 18 à 24 ans".
-
Représentez la situation à l'aide d'un arbre pondéré.
Corrigé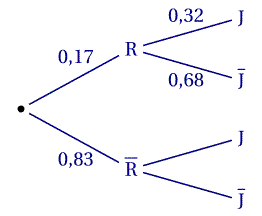
-
Calculer la probabilité P(R∩J).
Corrigé\[\begin{aligned} P(R\cap J) &= P(R)\times P_R(J)&\\ &= 0,17 \times 0,32&\\ &=0,0544.& \end{aligned}\] Donc $P(R\cap J)\approx 0,054$. -
D'après cette même étude, les jeunes de 18 à 24 ans représentent 11 % de la population française.
Montrer que la probabilité que la personne interrogée soit un jeune de 18 à 24 ans n'utilisant pas régulièrement les transports en commun est 0,056 à 10−3 près.
CorrigéD'après l'énoncé, $P(J) = 0,11$, donc selon la formule des probabilités totales \[\begin{aligned} &P(R\cap J) + P(\overline R \cap J) = P(J)&\\ \iff&0,0544 + P(\overline R \cap J) = 0,11&\\ \iff &P(\overline R \cap J) = 0,11 - 0,0544&\\ \iff &P(\overline R \cap J) = 0,0556.& \end{aligned}\] Donc $P(\overline R \cap J) \approx 0,056$. -
En déduire la proportion de jeunes de 18 à 24 ans parmi les utilisateurs non réguliers
des transports en commun.
CorrigéOn cherche ici \[P_{\overline R}(J) = \frac{P(\overline R \cap J)}{P(\overline R)} = \frac{0,0556}{0,83} \approx 0,067.\] Il y a donc environ 6,7 % de jeunes parmi les utilisateurs non réguliers des transports en commun.
Partie B :
Lors d'un recensement sur la population française, un recenseur interroge au hasard 50 personnes en une journée sur leur pratique des transports en commun.
La population française est suffisamment importante pour assimiler ce recensement à un tirage avec remise.
Soit X la variable aléatoire dénombrant les personnes utilisant régulièrement les transports en commun parmi les 50 personnes interrogées.
-
Déterminer, en justifiant, la loi de X et préciser ses paramètres.
CorrigéPuisque ce sondage est assimilé à un tirage avec remise, $X$ suit la loi binomiale de paramètres $n = 50$ et $p=0,17$. -
Calculer P(X=5) et interpréter le résultat.
CorrigéD'après la calculatrice \[P(X = 5) \approx 0,069.\] -
Le recenseur indique qu'il y a plus de 95 % de chance pour que,
parmi les 50 personnes interrogées, moins de 13 d'entre elles utilisent régulièrement
les transports en commun.
Cette affirmation est-elle vraie ? Justifier votre réponse.
CorrigéD'après la calculatrice \[P(X\le 12) \approx 0,928\] C'est donc 93 %, soit moins que 95 %. Le recenseur a donc formellement tort. -
Quel est le nombre moyen de personnes utilisant régulièrement les transports en commun
parmi les 50 personnes interrogées ?
CorrigéL'espérance de $X$ est \[\operatorname E(X) = np = 50 \times 0,17 = 8,5.\] Donc, en moyenne, 8,5 personnes interrogées utilisent régulièrement les transports en commun.
retour
code : 801