02

retour

On considère le cube $ABCDEFGH$ d'arête de longueur 1.
L'espace est muni du repère orthonormé $\left(A,\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AE}\right)$.
Le point $I$ est le milieu du segment $[EF]$, $K$ le centre du carré $ADHE$ et $O$ le milieu du segment $[AG]$.

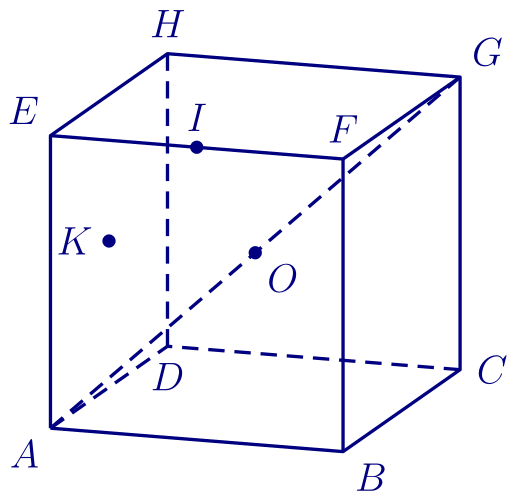
Le but de l'exercice est de calculer de deux manières différentes, la distance du point $B$ au plan $(AIG)$.

Partie 1. Première méthode

1. Donner, sans justification, les coordonnées des points $A$, $B$, et $G$.
Corrigé

$A(0;0;0)$, $B(1;0;0)$ et $G(1;1;1)$.

On admet que les points $I$ et $K$ ont pour coordonnées $I\left(\dfrac{1}{2};0;1\right)$ et $K\left(0;\dfrac{1}{2};\dfrac{1}{2}\right)$.

2. Démontrer que la droite $(BK)$ est orthogonale au plan $(AIG)$.
Corrigé

Les vecteurs $\overrightarrow{BK}$, $\overrightarrow{AI}$ et $\overrightarrow{AG}$ ont pour coordonnées \[\overrightarrow{GK} \begin{pmatrix}8 - 1\\\frac 1 2 - 0\\\frac 1 2 - 0\end{pmatrix} \implies \overrightarrow{GK}\begin{pmatrix}-1\\ \frac 1 2\\ \frac 1 2\end{pmatrix}, \quad\overrightarrow{AI}\begin{pmatrix}\frac 1 2\\0\\1 \end{pmatrix}, \quad\overrightarrow{AG} \begin{pmatrix}1\\1\\1\end{pmatrix}.\] Donc \[\begin{aligned} \overrightarrow{BK}\cdot\overrightarrow{AI} &=-1\cdot \frac 1 2 + 1\cdot 0 + \frac 1 2 \cdot 1 = 0&\\ \overrightarrow{BK}\cdot\overrightarrow{AG} &=-1\cdot 1 + \frac 1 2 \cdot 1 + \frac 1 2 \cdot 1 = 0& \end{aligned}\] Donc $\overrightarrow{BK}$, orthogonal à la base $(\overrightarrow{AI};\overrightarrow{AG})$ du plan $(AIG)$, est normal à ce plan.
La droite $(BK)$ qu'il dirige est donc perpendiculaire au plan $(AIG)$.

3. Vérifier qu'une équation cartésienne du plan $(AIG)$ est : \[2x - y - z = 0.\] Corrigé

le vecteur $-2\overrightarrow{BK}$ est un autre vecteur normal au plan $(AIG)$.
Ses coordonnées sont \[-2\overrightarrow{BK} : \begin{pmatrix}-2\cdot(-1)\\-2\cdot \frac 1 2\\-2\cdot \frac 1 2\end{pmatrix} =\begin{pmatrix}2\\-1\\-1\end{pmatrix}.\] Donc $(AIG)$ admet une équation cartésienne de la forme \[2x - y - z + d = 0.\] De plus, $A(0;0;0)$ appartient à ce plan, donc ses coordonnées en vérifient l'équation : \[2\times 0 - 0 - 0 + d= 0 \iff d = 0.\] Une équation cartésienne de $(AIG)$ est donc bien : \[2x - y - z = 0.\]

4. Donner une représentation paramétrique de la droite $(BK)$.
Corrigé

La droite $(BK)$ est dirigée par le vecteur $-2\overrightarrow{BK}\begin{pmatrix}2\\-1\\-1\end{pmatrix}$ et passe par le point $B(1;0;0)$.
Elle admet donc pour représentation paramétrique \[(BK):\begin{cases}x = 2t + 1\\y = -t\\z=-t\end{cases}, t\in\mathbb R.\]

5. En déduire que le projeté orthogonal $L$ du point $B$ sur le plan $(AIG)$ a pour coordonnées $L\left(\dfrac{1}{3};\dfrac{1}{3};\dfrac{1}{3}\right)$.
Corrigé

$L$ est l'intersection de la droite $(BK)$ avec le plan $(AIG)$.
Puisqu'il est sur $(BK)$, il existe un réel $t$ tel que \[\begin{cases}x_L = 2t + 1\\y_L = -t\\z_L = -t\end{cases}\] Puisqu'il est sur $(AIG)$, ses coordonnées vérifient l'équation \begin{align*} 2x_L - y_L - z_L &= 0& \\ \iff 2(2t+1)+t+t &= 0& \\ \iff t &= -\frac 2 6 = -\frac 1 3.& \end{align*} Donc : \[\begin{cases}x_L = 2t + 1=-\frac 2 3 + 1= \frac 1 3\\ y_L = \frac 1 3\\z_L = \frac 1 3\end{cases} \implies L\left(\frac 1 3;\frac 1 3;\frac 1 3\right)\]

6. Déterminer la distance du point $B$ au plan $(AIG)$.
Corrigé

La distance du point $B$ au plan $(AIG)$ est la longueur $BL$. \begin{align*} BL &=\sqrt{(x_L-x_B)^2 + (y_L - y_B)^2 + (z_L - z_B)^2}& \\ &=\sqrt{\left(\frac 1 3 - 1\right)^2 + \left(\frac 1 3 - 0\right)^2 + \left(\frac 1 3 - 0\right)^2}& \\ &=\sqrt{ \frac 4 9 + \frac 1 9 + \frac 1 9}& \\ &=\sqrt{\frac 6 9}& \\ &=\frac{\sqrt 6}{\sqrt 9}& \\ &=\frac{\sqrt 6} 3.& \end{align*}

Partie 2. Deuxième méthode

On rappelle que le volume $V$ d'une pyramide est donné par la formule \[V = \dfrac{1}{3} \times b \times h,\] où $b$ est l'aire d'une base et $h$ la hauteur associée à cette base.

1.a. Justifier que dans le tétraèdre $ABIG$, $[GF]$ est la hauteur relative à la base $AIB$.
Corrigé 1 Corrigé 2

Dans le cube, l'arête $[GF]$ est perpendiculaire au plan contenant la face $(ABF)$, donc orthogonale aux droites $(AB)$ et $(AI)$ incluses dans ce plan.
Elle est donc orthogonale à la face $(AIB)$ tout en passant par le sommet $G$.
C'est la hauteur de $ABIG$ relative à la face $ABI$.

Les vecteurs $\overrightarrow{FG}$, $\overrightarrow{AI}$ et $\overrightarrow{AB}$ ont pour coordonnées respectives \[\overrightarrow{FG}\begin{pmatrix}0\\1\\0\end{pmatrix},\quad \overrightarrow{AI}\begin{pmatrix}\frac 1 2\\0\\1\end{pmatrix},\quad \overrightarrow{AB}\begin{pmatrix}1\\0\\0\end{pmatrix}.\] Donc : \[\begin{aligned} \overrightarrow{EG}\cdot\overrightarrow{AI} &=\frac 1 2 \times 0 + 0 \times 1 + 1\times 0 = 0&\\ \overrightarrow{EG}\cdot\overrightarrow{AB} &=0\times 1 + 1\times 0 + 0\times 0 = 0& \end{aligned}\] Donc la droite $(EG)$ est bien orthogonale avec les droites $(AI)$ et $(AB)$, donc avec la face $(ABI)$. Elle passe de plus par le sommet $G$.
C'est la hauteur de $ABIG$ relative à la face $ABI$.

b. En déduire le volume du tétraèdre $ABIG$.
Corrigé

Dans le triangle $ABI$, soit $J$ le pied de la hauteur issue de $I$. $J$ est aussi le milieu de $[AB]$ car le triangle $ABI$ est isocèle en $I$.
On a donc $AB = IJ = 1$.
Alors l'aire du triangle $AIB$ est \[\mathcal A_{AIB} = \frac{AB\times IJ} 2 = \frac {1\times 1} 2 = \frac 1 2.\] $EF = 1$, donc finalement : \[\mathcal V_{ABIG} = \frac{\mathcal A_{ABI} \times EG} 3 = \frac{\frac 1 2 \times 1} 3 = \frac 1 6.\]

2. On admet que $AI = IG = \dfrac{\sqrt{5}}{2}$ et que $AG = \sqrt 3$.
Démontrer que l'aire du triangle isocèle $AIG$ est égale à $\dfrac{\sqrt{6}}{4}$ unité d'aire.
Corrigé

Puisque $AIG$ est isocèle en $I$, le pied de la hauteur issue de $I$ est le milieu de $[AG]$, autrement dit : \[O\left(\frac 1 2;\frac 1 2;\frac 1 2\right).\] Donc \begin{align*} OI &= \sqrt{\left(\frac 1 2 - \frac 1 2\right)^2 + \left(0 -\frac 1 2\right)^2 + \left(1 - \frac 1 2\right)^2}& \\ &=\sqrt{\frac 1 4 + \frac 1 4}& \\ &= \sqrt{\frac 2 4} = \frac {\sqrt{2}} 2.& \end{align*} Alors \[\mathcal A_{AIG} = \frac{AG\times OI}2 = \frac{\sqrt 3 \times \frac{\sqrt 2} 2} 2 =\frac{\sqrt{3\times 2}}{2\times 2} = \frac{\sqrt 6} 4.\]

3. En déduire la distance du point $B$ au plan $(AIG)$.
Corrigé

Notons $h$ la hauteur issue du sommet $B$ dans le tétraèdre $ABIG$: \begin{align*} \mathcal V_{ABIG} &=\frac{\mathcal A_{AIG} \times h} 3& \\ \iff \frac 1 6 &= \frac{\frac{\sqrt 6} 4 \times h} 3& \\ \iff \frac 1 2 &= h\frac{\sqrt 6} 4& \\ \iff \frac 1 2 \times \frac 4{\sqrt 6} &= h& \\ \iff \frac{2}{\sqrt 6} &= h& \\ \iff h &= \frac{2\sqrt 6} 6& \\ \iff h &= \frac{\sqrt 6} 3.& \end{align*} Or $h=\dfrac{\sqrt 6} 3$ n'est autre que la distance du point $B$ au plan $(AIG)$.

retour

code : 800