7.12

retour

Cet exercice est un QCM. Pour chaque question, une et une seule réponse est correcte.

1. On considère la fonction $f$ définie et dérivable sur $]0;+\infty[$ par : \[f(x) = x \ln(x) - x + 1.\] Parmi les quatre expressions suivantes, laquelle est celle de la fonction dérivée de $f$ ?

a. $\ln (x)$;
b.$\dfrac{1}{x} - 1$;
c. $\ln (x) - 2$;
d. $\ln (x) - 1$.
Corrigé

Réponse a. \[f'(x) = 1\cdot \ln x + x\cdot \frac 1 x - 1 + 0 =\ln x + 1 - 1 =\ln x.\]

2. On considère la fonction $g$ définie sur $]0;+\infty[$ par \[g(x) = x^2[1 - \ln (x)].\] Parmi les quatre affirmations suivantes, laquelle est correcte ?
a. $\displaystyle\lim_{x \to 0} g(x) = +\infty$;
b. $\displaystyle\lim_{x \to 0} g(x) = - \infty$;
c.c. $\displaystyle\lim_{x \to 0} g(x) = 0$;
d. La fonction $g$ n'admet pas de limite en 0.
Corrigé

Réponse c. En effet \[g(x) = x^2 - x^2\ln x\] avec \[\lim_{x\to 0} x^2 = 0 \quad\text{et}\quad \lim_{x\to 0} x^2\ln x = 0\ \text{(limite spéciale du cours)}.\] Donc: \[\lim_{x\to 0} x^2 - x^2\ln x = 0 - 0 = 0.\] On peut vérifier en observant la représentation graphique de $g$ à la calculatrice.

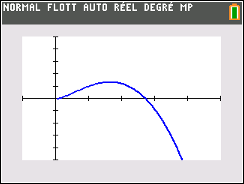
3. On considère la fonction $f$ définie sur $\mathbb R$ par \[f(x) = x^3 - 0,9x^2 -0,1x.\] Le nombre de solutions de l'équation $f(x) = 0$ sur $\mathbb R$ est :
a. $0$;
b. $1$;
c. $2$;
d. $3$.
Corrigé

Réponse d. Pour tout réel $x$: \[f(x) = x^3 - 0,9x^2 - 0,1x = x(x^2 - 0,9x - 0,1).\] Donc $f(x) = 0$ si et seulement si $x=0$ (une solution) ou $x$ est solution de \[x^2 - 0,9x - 0,1 = 0.\] Le discriminant de ce polynôme est : \[\Delta = (-0,9)^2 - 4\times 1 \times (-0,1) = 1,21.\] $\Delta > 0$, donc il y a deux autres solutions. Au total, on en a donc 3.
(Les solutions sont $-0,1$, $0$ et $1$. Deux solutions, proches l'une de l'autre, risquent de ne pas être distinguables sur une représentation graphique)

4. Si $H$ est une primitive d'une fonction $h$ définie et continue sur $\mathbb R$, et si $k$ est la fonction définie sur $\mathbb R$ par \[k(x) = h(2x),\] alors, une primitive $K$ de $k$ est définie sur $\mathbb R$ par :
a. $K(x) =H(2x)$;
b. $K(x) =2H(2x)$;
c. $K(x) =\dfrac{1}{2}H(2x)$;
d. $K(x) =2H(x)$.
Corrigé

Réponse c. Dérivons $x\mapsto H(2x)$ \begin{align*} &\left(H(2x)\right)' = 2H'(2x) = 2h(2x)& \\ \Rightarrow &\left(\frac 1 2H(2x)\right)' = \frac 1 2 \cdot 2h(2x) = h(2x).& \end{align*} Donc une primitive de $k$ est $x\mapsto \dfrac 1 2 H(2x)$.

5. L'équation réduite de la tangente au point d'abscisse 1 de la courbe de la fonction $f$ définie sur $\mathbb R$ par \[f(x) = x\mathrm{e}^x\] est :
a. $y = \mathrm{e}x + \mathrm{e}$;
b. $y =2\mathrm{e}x - \mathrm{e}$;
c. $y = 2\mathrm{e}x + \mathrm{e}$;
d. $y = \mathrm{e}x$.
Corrigé

Réponse b. Pour tout réel $x$: \[f'(x) = 1\cdot\mathrm e^x + x\mathrm e^x \implies f'(1) = \mathrm e^1 + \mathrm e^1 = 2\mathrm e.\] D'autre part, $f(1)= 1\mathrm e^1 = \mathrm e$.
Donc l'équation de la tangente est : \begin{align*} &y = f'(1)(x-1)+f(1)& \\ \iff &y = 2\mathrm e(x-1)+\mathrm e& \\ \iff &\boxed{y = 2\mathrm e^x - \mathrm e.}& \end{align*}

6. Les nombres entiers $n$ solutions de l'inéquation \[(0,2)^n < 0,001\] sont tous les nombres entiers $n$ tels que :
a. $n \leqslant 4$;
b. $n\leqslant 5$;
c. $n \geqslant 4$;
d. $n \geqslant 5$.
Corrigé

Réponse d. On peut faire des essais à la calculatrice ou résoudre : \begin{align*} 0,2^n &< 0,001& \\ \iff \ln(0,2^n) &< \ln(0,001)& \\ \iff n \ln(0,2) &<\ln(0,001)& \\ \iff n &> \frac{\ln(0,001)}{\ln(0,2)}.& \end{align*} Puisque $\dfrac{\ln(0,001)}{\ln(0,2)} \approx 4,29$, cela équivaut à $n \ge 5$.

retour

code : 797