retour

Un hôtel situé à proximité d'un site touristique dédié à la préhistoire propose deux visites dans les environs, celle d'un musée et celle d'une grotte.

Une étude a montré que 70 % des clients de l'hôtel visitent le musée. De plus, parmi les clients visitant le musée, 60 % visitent la grotte.
Cette étude montre aussi que 6 % des clients de l'hôtel ne font aucune visite.

On interroge au hasard un client de l'hôtel et on note :

• $M$ l'évènement : «le client visite le musée»;
• $G$ l'évènement : «le client visite la grotte».

1. 1. Vérifier que $p_{\overline{M}}\left(\overline{G}\right) = 0,2$.
      Corrigé
      D'après la consigne, \[p(M)=0,7,\ p_M(G) = 0,6,\ p(\overline M\cap\overline G) = 0,06.\]
      Alors \[p_{\overline M}(\overline G) = \frac{p(\overline M\cap \overline G)}{p(\overline M)} =\frac{0,06}{1-0,7} =\frac{0,06}{0,3} =0,2.\]
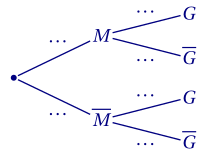
   2. L'arbre pondéré ci-dessous modélise la situation. Recopier et compléter cet arbre en indiquant sur chaque branche la probabilité associée.
      
      Corrigé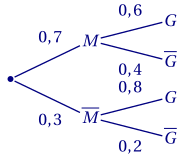
      
   3. Quelle est la probabilité de l'évènement «le client visite la grotte et ne visite pas le musée» ?
      Corrigé
      \[p(\overline M\cap G) = p(\overline M)\times p_{\overline M}(G) = 0,3 \times 0,8 = 0,24.\]
   4. Montrer que $p(G) = 0,66$.
      Corrigé
      \[\begin{aligned} p(G) &= p(M\cap G) + p(\overline M \cap G)& \\ &=p(M)\times p_M(G) + p(\overline M \cap G)& \\ &= 0,7 \times 0,6 + 0,24& \\ &=0,66.& \end{aligned}\]
2. Le responsable de l'hôtel affirme que parmi les clients qui visitent la grotte, plus de la moitié visitent également le musée. Cette affirmation est-elle exacte ?
   Corrigé
   Nous cherchons \[p_G(M) = \frac{p(M\cap G)}{p(G)} = \frac{0,421}{0,66} \approx 0,636\] $p_G(M) > 0,5$ donc l'affirmation est vraie.
3. Les tarifs pour les visites sont les suivants :
   • visite du musée : 12 euros ;
   • visite de la grotte : 5 euros.
   On considère la variable aléatoire $T$ qui modélise la somme dépensée par un client de l'hôtel pour ces visites.
   1. Donner la loi de probabilité de $T$. On présentera les résultats sous la forme d'un tableau.
      Corrigé
      $T$ prend les valeurs $0$, $5$, $12$ et $12+5=17$. \[\begin{array}{|l|c|c|c|c|} \hline t & 0 & 5 & 12 & 17 \\ \hline \text{Év.}\rule{0em}{1.2em} &\overline M\cap \overline G & \overline M \cap G &M\cap \overline G & M\cap G \\ \hline p(T=t) & 0,06 & 0,24 & 0,28 & 0,42 \\ \hline \end{array}\]
   2. Calculer l'espérance mathématique de $T$.
      Corrigé
      \[\begin{aligned} \operatorname E(T) &= 0,06\times 0 + 0,24\times 5 + 0,28\times 12 + 0,42\times 17& \\ &= 11,70.& \end{aligned}\] Donc l'espérance est de 11,70 €.
   3. Pour des questions de rentabilité, le responsable de l'hôtel estime que le montant moyen des recettes des visites doit être supérieur à 700 euros par jour.
      Déterminer le nombre moyen de clients par journée permettant d'atteindre cet objectif.
      Corrigé
      On peut considérer que chaque client rapporte en moyenne 11,70 €. Donc le nombre $n$ de clients doit vérifier \[11,7n \gt 700 \iff n \gt\frac{700}{11,7}.\] Or \[\dfrac{700}{11,7}\approx 59,83,\] donc le nombre de client doit être au moins égal à 60.
4. Pour augmenter les recettes, le responsable souhaite que l'espérance de la variable aléatoire modélisant la somme dépensée par un client de l'hôtel pour ces visites passe à 15 euros, sans modifier le prix de visite du musée qui demeure à 12 euros.
   Quel prix faut-il fixer pour la visite de la grotte afin d'atteindre cet objectif ? (On admettra que l'augmentation du prix d'entrée de la grotte ne modifie pas la fréquentation des deux sites).
   Corrigé
   Soit $x$ le prix de la visite de la grotte. On veut que \[\begin{aligned} &0,24x + 0,28\times 12 + 0,42(x+12)=15& \\ \iff &0,24x + 3,36 + 0,42x + 5,04 = 15& \\ \iff &0,66x = 6,6& \\ \iff &x = \frac{6,6}{0,66} = 10.& \end{aligned}\] Il faut donc passer le prix de la visite de la grotte à 10 €.
5. On choisit au hasard 100 clients de l'hôtel, en assimilant ce choix à un tirage avec remise.
   Quelle est la probabilité qu'au moins les trois quarts de ces clients aient visité la grotte à l'occasion de leur séjour à l'hôtel ?
   On donnera une valeur du résultat à 10⁻³ près.
   Corrigé
   Puisque les choix de clients sont assimilés à un tirage avec remise, le nombre $X$ de clients ayant visité la grotte suit la loi binomiale de paramètres $n = 100$ et $p=0,66$.
   On cherche \[p(X\ge 75) = 1- p(\le 74) \approx 1 - 0,966 \approx 0,034.\]

retour

code : 795