retour

Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.
q Aucune justification n'est demandée.

1. On considère la fonction $g$ définie sur $\mathbb R$ par : \[ g(x) = \dfrac{2\mathrm{e}^x}{\mathrm{e}^x +1}.\] La courbe représentative de la fonction $g$ admet pour asymptote en $+\infty$ la droite d'équation :
   1. $x = 2$;
   2. $y = 2$;
   3. $y = 0$;
   4. $x = - 1$.
   Corrigé
   Réponse b. Un tracé de la courbe de cette fonction à la calculatrice permet de répondre rapidement à cette question.
   Si on veut le prouver, pour tout réel $x$ : \[ g(x) = \frac{2\mathrm e^x}{\mathrm e^x + 1} =\frac{2\mathrm e^x}{\mathrm e^x\left(1+\frac 1{\mathrm e^x}\right)} =\frac{2}{1+\mathrm e^{-x}}. \] Alors : \[\begin{aligned} &\lim_{x\to+\infty} -x = -\infty& \\ \implies &\lim_{x\to+\infty} \mathrm e^{-x} = 0& \\ \implies &\lim_{x\to+\infty} \frac 2 {1+\mathrm e^{-x}} = \frac 2 {1+0} = 2.& \end{aligned}\] La droite d'équation $y =2$ est donc asymptote à la courbe de $g$ en $+\infty$.
2. On considère une fonction $f$ définie et deux fois dérivable sur $\mathbb R$.
   On appelle $\mathscr{C}$ sa représentation graphique.
   On a représenté sur le graphique ci-dessous la courbe de $f''$, notée $\mathscr{C}''$.
   
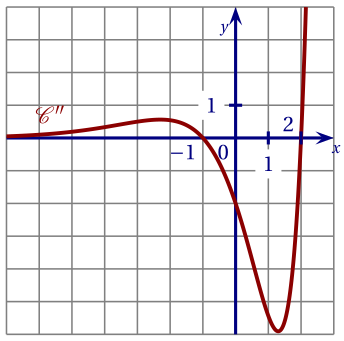
   1. $\mathscr{C}$ admet un unique point d'inflexion ;
   2. $f$ est convexe sur l'intervalle $[-1~;~2]$ ;
   3. $f$ est convexe sur $]-\infty;-1]$ et sur $[2;+\infty[$ ;
   4. $f$ est convexe sur $\mathbb R$.
   Corrigé
   Réponse c. En effet :
   $f''$ change deux fois de signe, donc il y a deux points d'inflexion.
   $f''\le 0$ sur $[-1;2]$ donc $f$ est concave sur cet intervalle.
   $f'' \ge 0$ sur $]-\infty;-1]$ et $[2;+\infty[$, donc $f$ est bien convexe sur ces intervalles.
3. On donne la suite $\left(u_n\right)$ définie par: $u_0=0$ et pour tout entier naturel $n$, \[u_{n+1} = \dfrac 1 2 u_n + 1.\] La suite $\left(v_n\right)$, définie pour tout entier naturel $n$ par $v_n = u_n-2$, est :
   1. arithmétique de raison $-2$ ;
   2. géométrique de raison $-2$ ;
   3. arithmétique de raison 1 ;
   4. géométrique de raison $\dfrac 1 2$.
   Corrigé
   Réponse d. En effet, pour tout entier naturel $n$ : \[\begin{aligned} v_{n+1} &=u_{n+1} - 2& \\ &=\frac 1 2 u_n + 1 - 2& \\ &=\frac 1 2 u_n - 1& \\ &=\frac 1 2 \left(u_n - 2\right)& \\ &=\frac 1 2 v_n.& \end{aligned}\]
4. On considère une suite $\left(u_n\right)$ telle que, pour tout entier naturel, on a : \[1 + \left(\dfrac 1 4\right)^n \leqslant u_n \leqslant 2 - \dfrac{n}{n+1}\] On peut affirmer que la suite $\left(u_n\right)$ :
   1. converge vers 2 ;
   2. converge vers 1 ;
   3. diverge vers $+\infty$ ;
   4. n'a pas de limite.
   Corrigé
   Réponse b. Une étude à la calculatrice permet de conjecturer que les suites encadrantes tendent toutes deux vers 1, donc qu'il en va de même pour la suite $(u_n)$.
   Preuve. Puisque $\dfrac 1 4\in]-1;1[$, \[\lim_{n\to+\infty} \left(\frac 1 4\right)^n = 0 \implies \lim_{n\to+\infty} 1+ \left(\frac 1 4\right)^n = 1.\] D'autre part, pour $n\neq 0$: \[\frac{n}{n+1} = \frac{n}{n\left(1+\frac 1 n\right)} =\frac{1}{1+\frac 1 n}.\] Alors : \[\lim_{n\to+\infty} \frac 1 n = 0 \implies \lim_{n\to+\infty} \frac 1 {1+\frac 1 n} = \frac 1 {1+0} = 1.\]
5. Soit $f$ la fonction définie sur $]0;+\infty[$ par \[f(x) = x^2 \ln x.\] Une primitive $F$ de $f$ sur $]0;+\infty[$ est définie par :
   1. \[F(x) = \dfrac 1 3 x^3 \left(\ln x - \dfrac 1 3 \right);\]
   2. \[F(x) = \dfrac 1 3 x^3 (\ln x - 1);\]
   3. \[F(x) = \dfrac 1 3 x^2;\]
   4. \[F(x) = \dfrac 1 3 x^2 (\ln x - 1).\]
   Corrigé
   Réponse a. En effet, dans ce cas \[\begin{aligned} F'(x) &= \frac 1 3 \cdot 3x^2\left(\ln x - \frac 1 3\right) + \frac 1 3x^3\cdot \frac 1 x& \\ &=x^2\ln x - x^2 + x^2 = x^2\ln x& \\ &= f(x).& \end{aligned}\] Puisque $F'=f$, $F$ est bien une primitive de $f$.
6. Pour tout réel $x$, l'expression \[2 + \dfrac{3\mathrm{e}^{-x} - 5}{\mathrm{e}^{-x} + 1}\] est égale à :
   1. \[\dfrac{5 - 3\mathrm{e}^x}{1 + \mathrm{e}^x};\]
   2. \[\dfrac{5 + 3\mathrm{e}^x}{1 - \mathrm{e}^x};\]
   3. \[\dfrac{5 + 3\mathrm{e}^x}{1 + \mathrm{e}^x};\]
   4. \[\dfrac{5 - 3\mathrm{e}^x}{1 - \mathrm{e}^x}.\]
   Corrigé
   Réponse a. On peut comparer à la calculatrice les courbes de \[x\mapsto 2+\dfrac{3\mathrm e^{-x}-5}{\mathrm e^{-x}+1} \ \text{et}\ x\mapsto \dfrac{5-3\mathrm e^{x}}{1+\mathrm e^x}\] et constater qu'elles sont identiques.
   Sinon, on peut réaliser le calcul suivant : \[\begin{aligned} 2+\frac{3\mathrm e^{-x}-5}{\mathrm e^{-x} + 1} &=2 + \frac{\mathrm e^{-x}\left(3 - \frac{5}{\mathrm e^{-x}}\right)}{\mathrm e^{-x}\left(1 + \frac{1}{\mathrm e^{-x}}\right)}& \\ &=2 + \frac{3-5\mathrm e^x}{1+\mathrm e^{x}}& \\ &=\frac{2\left(1+\mathrm e^{x}\right)+3-5\mathrm e^x}{1+\mathrm e^x}& \\ &=\frac{2 + 2\mathrm e^x + 3 - 5\mathrm e^x}{1+\mathrm e^x}& \\ &=\frac{5-3\mathrm e^x}{1+\mathrm e^x}.& \end{aligned}\]

retour

code : 794