retour

Pour préparer l'examen du permis de conduire, on distingue deux types de formation :

• la formation avec conduite accompagnée ;
• la formation traditionnelle.

On considère un groupe de 300 personnes venant de réussir l'examen du permis de conduire. Dans ce groupe :
75 personnes ont suivi une formation avec conduite accompagnée; parmi elles, 50 ont réussi l'examen à leur première présentation et les autres ont réussi à leur deuxième présentation.
225 personnes se sont présentées à l'examen suite à une formation traditionnelle; parmi elles, 100 ont réussi l'examen à la première présentation, 75 à la deuxième et 50 à la troisième présentation.

On interroge au hasard une personne du groupe considéré. On considère les événements suivants :
$A$ : « la personne a suivi une formation avec conduite accompagnée » ;
$R_1$ : « la personne a réussi l'examen à la première présentation » ;
$R_2$ : « la personne a réussi l'examen à la deuxième présentation » ;
$R_3$ : « la personne a réussi l'examen à la troisième présentation ».

1. Modéliser la situation par un arbre pondéré.
   Corrigé
   Arbre pondéré (les effectifs sont rappelés entre parenthèses) :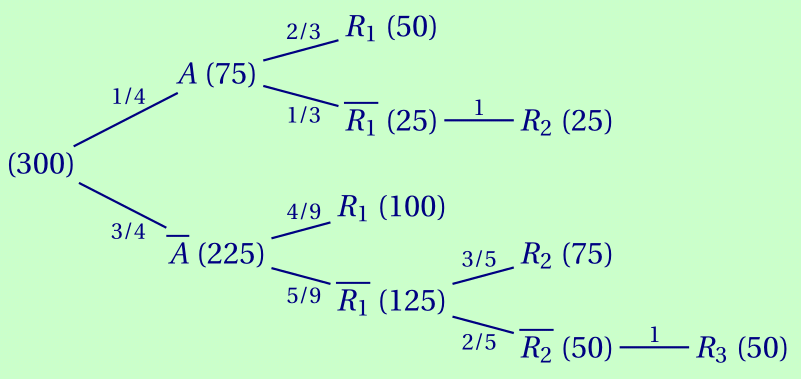

   
2. 1. Calculer la probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l'examen à sa deuxième présentation.
      Corrigé
      En utilisant les effectifs donnés : \[P(A\cap R_2) = \dfrac{25}{300} = \dfrac 1 {12}.\] En utilisant l'arbre : \[P(A\cap R_2) = \dfrac 1 4 \times \dfrac 1 3 \times 1 = \dfrac 1 {12}.\]
   2. Montrer que la probabilité que la personne interrogée ait réussi l'examen à sa deuxième présentation est égale à $\dfrac 1 3$.
      Corrigé
      En utilisant les effectifs donnés : \[P(R_2) = \dfrac{25+75}{300} = \dfrac 1 3.\] En utilisant l'arbre : \[P(R_2) = \dfrac 1 {12} + \dfrac 3 4 \times \dfrac 5 9 \times \dfrac 3 5 = \dfrac 1 3.\]
   3. La personne interrogée a réussi l'examen à sa deuxième présentation.
      Quelle est la probabilité qu'elle ait suivi une formation avec conduite accompagnée ?
      Corrigé
      \[P_A(R_2) = \dfrac{P(A\cap R_2)}{P(A)} = \dfrac{\frac 1 {12}}{\frac 1 3} = \dfrac 1 {12}\times \dfrac 3 1 = \dfrac 1 4.\]
3. On note $X$ la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s'est présentée à l'examen jusqu'à sa réussite.
   Ainsi, $\{X = 1\}$ correspond à l'événement $R_1$.
   1. Déterminer la loi de probabilité de la variable aléatoire $X$.
      Corrigé
      Tous les candidats ont leur permis en au plus trois essais, donc \[X\in\{1;2;3\}.\] On sait déjà que \[P(X=2) = P(R_2) = \dfrac 1 3.\] De plus \[P(X=1) = P(R_1) =\dfrac{50+100}{300} = \dfrac 1 2.\] Donc \[P(X=3) = 1 - \dfrac 1 2 - \dfrac 1 3 = \dfrac 1 6.\] En résumé : En résumé : \[\begin{array}{|l|c|c|c|} \hline x_i & 1 & 2 & 3& \\ \hline P(X=x_i) \rule[-.5em]{0em}{1.6em}& \frac 1 2 & \frac 1 3 & \frac 1 6 \\ \hline \end{array}\]
   2. Calculer l'espérance de cette variable aléatoire. Interpréter cette valeur dans le contexte de l'exercice.
      Corrigé
      \[\operatorname{E}(X) = \dfrac 1 2 \times 1 + \dfrac 1 3 \times 2 + \dfrac 1 6 \times 3 = \dfrac 5 3.\] C'est, en moyenne, le nombre de tentatives nécessaires à un candidat pour obtenir son permis.
4. On choisit, successivement et de façon indépendante, $n$ personnes parmi les 300 du groupe étudié, où $n$ est un entier naturel non nul.
   On assimile ce choix à un tirage avec remise de $n$ personnes parmi les 300 personnes du groupe.
   On admet que la probabilité de l'événement $R_3$ est égale à $\dfrac 1 6$.
   1. Dans le contexte de cette question, préciser un événement dont la probabilité est égale à \[1 - \left(\dfrac 5 6\right)^n.\] Corrigé
      Puisque $P(R_3) = \dfrac 1 6$, \[\dfrac 5 6 = 1 - \dfrac 1 6 = P(\overline{R_3}).\] Donc \[\left(\dfrac 5 6\right)^n\] est la probabilité qu'aucun des $n$ candidats choisis n'ait eu son permis au troisième essai. \[1 - \left(\dfrac 5 6\right)^n\] est donc la probabilité de l'événement contraire, à savoir « au moins un des $n$ candidats a eu son permis à son troisième essai ».
   2. On considère la fonction Python seuil ci-dessous, où p est un nombre réel appartenant à l'intervalle ]0 ; 1[.
      
      def seuil(p): n = 1 while 1-(5/6)**n <= p : n = n+1 return n
      Quelle est la valeur renvoyée par la commande seuil(0.9) ?
      Interpréter cette valeur dans le contexte de l'exercice.
      Corrigé : valeur renvoyée (main)
      Exécutons le programme à la main. La trace (abrégée) de cette exécution est donnée ci-dessous. \[\small \begin{array}{|l|c|c|c|c|c|}\hline n & 1 & 2 & \cdots & 12 & 13 \\ \hline 1- (5/6)^n & 0,167 & 0,306 & \cdots & 0,888 & 0,907 \\ \hline 1-(5/6)^n \le p\ ? &\text{oui} & \text{oui} & \cdots &\text{oui}& \text{non} \\ \hline \end{array}\] Donc le programme renvoi la valeur $n=13$.
      
      Corrigé : valeur renvoyée (avec ln)
      La valeur renvoyée par le programme est le plus petit entier naturel $n$ tel que \begin{align*} 1 - \left(\frac 5 6\right)^n &> p& \\ \iff 1-\left(\frac 5 6\right)^n &> 0,9& \\ \iff -\left(\frac 5 6\right)^n &> -0,1& \\ \iff \left(\frac 5 6\right)^n &< 0,1& \\ \iff \ln\left[\left(\frac 5 6\right)^n\right] &< \ln(0,1)& \\ \iff n\ln\left(\frac 5 6 \right) &< \ln(0,1)& \\ \iff n &> \frac{\ln(0,1)}{\ln(5/6)}.& \end{align*} Sachant que $\dfrac{\ln(0,1)}{\ln(5/6)}\approx 12,62$, l'algorithme renverra l'entier $n=13$.
      
      Corrigé : interprétation
      Il faut donc choisir au moins 13 candidats pour que la probabilité qu'au moins l'un d'entre eux ai réussi son permis au troisième essai soit supérieure à 0,9.

retour

code : 793