7.10
retour
Partie A
On considère la fonction $f$ définie pour tout réel $x$ de $]0;1]$ par : \[f(x) = \mathrm{e}^{-x} + \ln (x).\]
1.
Calculer la limite de $f$ en $0$.
Corrigé
2.
On admet que $f$ est dérivable sur $]0;1]$. On note $f'$ sa fonction dérivée.
3.
Justifier que, pour tout réel $x$ appartenant à $]0;1]$, on a
\[x\mathrm{e}^{-x} < 1.\]
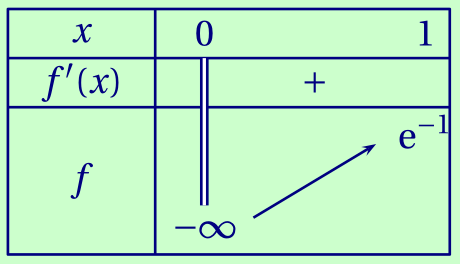
En déduire le tableau de variation de $f$ sur $]0;1]$.
Corrigé
Ajoutons que \[f(1) = \mathrm e^{-1} + \ln(1) = \mathrm e^{-1}\] et l'on peut établir le tableau de variation suivant.
4.
Démontrer qu'il existe un unique réel $\ell$ appartenant à $]0;1]$ tel que $f(\ell) = 0$.
Corrigé
Donc tout réel de l'intervalle $\left]-\infty;\mathrm e^{-1}\right]$ admet un antécédent par $f$. C'est donc en particulier le cas de $0$.
De plus, $f$ est strictement croissante sur cet intervalle, donc cet antécédent est unique. L'équation $f(x) = 0$ admet donc une unique solution dans $]0;1]$.
Partie B.
1. On définit deux suites $\left(a_n\right)$ et $\left(b_n\right)$ par : \[\left\{\begin{array}{l c l} a_0& =& \dfrac{1}{10}\\ b_0& =& 1 \end{array}\right.\] et, pour tout entier naturel $n$, \[\left\{\begin{array}{l c l} a_{n+1}&=&\mathrm{e}^{-b_n}\\ b_{n+1}&=&\mathrm{e}^{-a_n} \end{array}\right.\]
a.
Calculer $a_1$ et $b_1$. On donnera des valeurs approchées à $10^{-2}$ près.
Corrigé
b. On considère ci-dessous la fonction termes, écrite en langage Python.
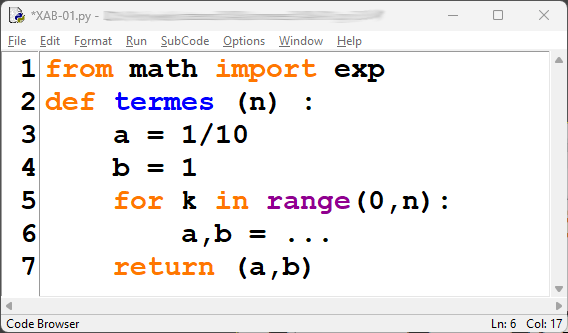
Corrigé
2. On rappelle que la fonction $x \mapsto \mathrm{e}^{-x}$ est décroissante sur $\mathbb R$.
a. Démontrer par récurrence que, pour tout entier naturel $n$, on a: \[0 < a_n \leqslant a_{n+1} \leqslant b_{n+1} \leqslant b_n \leqslant 1\] Corrigé
Puisque $a_0 = 1$, $a_1 \approx 0,37$, $b_1 \approx 0,9$ et $b_0 = 1$, on a bien \[0 < a_0 \le a_1 \le b_1 \le b_0 \le 1.\] Donc $\mathcal A(0)$ est vraie (initialisation).
Supposons donc maintenant que pour un entier naturel $n$ donné, $\mathcal A(n)$ est vraie. Cela signifie que \[0 < a_n \le a_{n+1} \le b_{n+1} \le b_n \le 1.\] On a admis que $\varphi:x\mapsto \mathrm e^{-x}$ est décroissante sur $\mathbb R$, donc: \[\begin{aligned} &0 < a_n \le a_{n+1} \le b_{n+1} \le b_n \le 1& \\ \implies &\varphi(1) \le \varphi(b_n) \le \varphi(b_{n+1}) \le \varphi(a_{n+1}) < \varphi(0)& \\ \implies &\varphi(1) \le a_{n+1} \le a_{n+2} \le b_{n+2} \le b_{n+1} < \varphi(0).& \end{aligned}\] Or \[\begin{aligned} &\begin{cases} \varphi(1) = \mathrm e^{-1} > 0\\ \varphi(0) = \mathrm e^0 = 1 \end{cases}& \\ \implies &0 < a_{n+1} \le a_{n+2} \le b_{n+2} \le b_{n+1} \le 1& \end{aligned}\] On a donc prouvé que $\mathcal A(n) \implies \mathcal A(n+1)$ (hérédité).
Donc, par récurrence, $\mathcal A(n)$ est vraie pour tout entier naturel $n$.
b. En déduire que les suites $\left(a_n\right)$ et $\left(b_n\right)$ sont convergentes. Corrigé
De même, la suite $(b_n)$ est décroissante et minorée par $0$.
Ces deux suites sont donc convergentes.
3.
On note $A$ la limite de $\left(a_n\right)$ et $B$ la limite de $\left(b_n\right)$.
On admet que $A$ et $B$ appartiennent à l'intervalle $]0\;;\;1]$, et que
\[
\begin{cases}A = \mathrm{e}^{-B}\\
B = \mathrm{e}^{-A}.
\end{cases}
\]
a.
Démontrer que $f(A) = 0$.
Corrigé
b.
Déterminer $A - B$.
Corrigé
Or on a montré en A.4. que cette équation n'a qu'une solution sur cet intervalle. Donc: \[A = B \implies A - B = 0.\] (Les suites $(a_n)$ et $(b_n)$ convergent vers une même limite.)
retour
code : 791