777
retour
$ABCDEFGH$ est le cube représenté ci-dessous.
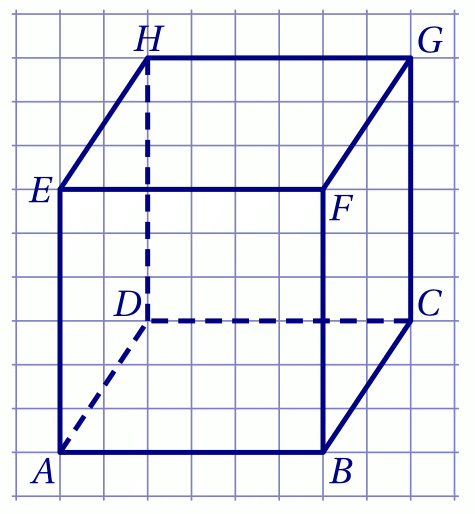
$I$, $J$ et $K$ sont les points définis par \[\begin{aligned} \overrightarrow{AI}&=\frac 1 2 \overrightarrow{AB}+\overrightarrow{AC},& \\ \overrightarrow{AJ}&=\overrightarrow{AC} + \frac 1 2\overrightarrow{AE},& \\ \overrightarrow{AK}&=\overrightarrow{AB}+ \frac 1 2 \overrightarrow{AE}.& \end{aligned}\]
-
Placer les points $I$, $J$ et $K$.
Corrigé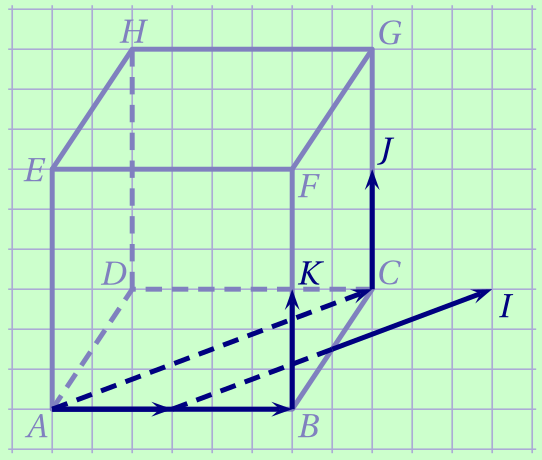
-
-
Démontrer que $\overrightarrow{IJ} =
\dfrac 1 2 \overrightarrow{BE}$.
Corrigé\begin{align*} \overrightarrow{IJ} &=\overrightarrow{IA}+\overrightarrow{AJ}& \\ &=-\left(\frac 1 2 \overrightarrow{AB}+\overrightarrow{AC}\right) +\left(\overrightarrow{AC}+\frac 1 2 \overrightarrow{AE}\right)& \\ &=-\frac 1 2\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AC} +\frac 1 2 \overrightarrow{AE}& \\ &=\frac 1 2 \overrightarrow{BA}+\frac 1 2 \overrightarrow{AE}& \\ &=\frac 1 2 \left(\overrightarrow{BA}+\overrightarrow{AE}\right)& \\ &=\frac 1 2 \overrightarrow{BE}.& \end{align*} -
Que peut-on en déduire pour les droites $(IJ)$ et $(BE)$?
Corrigé$\overrightarrow{IJ}$ et $\overrightarrow{BE}$ sont colinéaires, donc les droites $(IJ)$ et $(BE)$ sont parallèles.
-
Démontrer que $\overrightarrow{IJ} =
\dfrac 1 2 \overrightarrow{BE}$.
-
Les droites $(JK)$ et $(BC)$ sont-elles parallèles ? Justifier.
Corrigé\begin{align*} \overrightarrow{JK} &=\overrightarrow{JA}+\overrightarrow{AK}& \\ &=-\left(\overrightarrow{AC}+\frac 1 2 \overrightarrow{AE}\right) +\overrightarrow{AB}+\frac 1 2 \overrightarrow{AE}& \\ &=-\overrightarrow{AC}-\frac 1 2 \overrightarrow{AE} + \overrightarrow{AB} + \frac 1 2 \overrightarrow{AE}& \\ &=\overrightarrow{CA}+\overrightarrow{AB}& \\ &=\overrightarrow{CB}& \\ &=-\overrightarrow{BC}.& \end{align*} Les vecteurs $\overrightarrow{JK}$ et $\overrightarrow{BC}$ sont colinéaires, donc les droites $(JK)$ et $(BC)$ sont parallèles.
retour
code : 777