776
retour
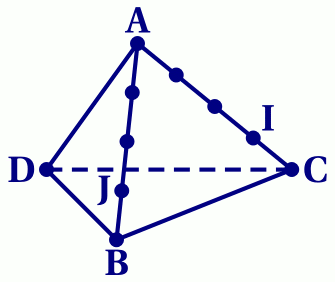
Dans le tétraèdre ABCD représenté ci-dessous, on a placé les points I et J tels que \[\overrightarrow{\mathrm{AI}} = \dfrac 3 4 \overrightarrow{\mathrm{AC}} \quad\text{et}\quad \overrightarrow{\mathrm{AJ}} = \dfrac 3 4 \overrightarrow{\mathrm{AB}} \]
-
Montrer que $\overrightarrow{\mathrm{JI}} = \dfrac 3 4 \overrightarrow{\mathrm{BC}}$.
CorrigéD'après la relation de Chasles: \begin{align*} \overrightarrow{\mathrm{JI}} =&\overrightarrow{\mathrm{JA}}+\overrightarrow{\mathrm{AI}} =\frac 3 4\overrightarrow{\mathrm{BA}} + \frac 3 4\overrightarrow{\mathrm{AC}} =\frac 3 4\left(\overrightarrow{\mathrm{BA}}+\overrightarrow{\mathrm{AC}}\right)& \\ =&\frac 3 4\overrightarrow{\mathrm{BC}}.& \end{align*} -
Que peut on en déduire pour la droite $(\mathrm{IJ})$ et le plan $(\mathrm{BCD})$?
CorrigéPuisque $\overrightarrow{\mathrm{JI}}$ et $\overrightarrow{\mathrm{BC}}$ sont colinéaires, les droites $(\mathrm{IJ})$ et $(\mathrm{BC})$ sont parallèles.
La droite $(\mathrm{BC})$ étant incluse dans le plan $(\mathrm{BCD})$, la droite $(\mathrm{IJ})$ est donc parallèle au plan $(\mathrm{BCD})$. -
On considère les points E et F tels que
\[\overrightarrow{\mathrm{AE}}=\overrightarrow{\mathrm{BC}}
\quad\text{et}\quad
\overrightarrow{\mathrm{AF}}=\overrightarrow{\mathrm{BD}}.\]
-
$\left(\overrightarrow{\mathrm{BC}},\overrightarrow{\mathrm{BD}}\right)$
est-elle une base du plan $(\mathrm{BCD})$?
CorrigéLes vecteurs $\overrightarrow{\mathrm{BC}}$ et $\overrightarrow{\mathrm{BD}}$ dirigent les droites sécantes $(\mathrm{BD})$ et $(\mathrm{BC})$; ils ne sont donc pas colinéaires et forment bien une base du plan $(\mathrm{BCD})$. -
Que peut-on dire des plans $(\mathrm{AEF})$ et $(\mathrm{BCD})$?
Corrigé$(\overrightarrow{\mathrm{AE}},\overrightarrow{\mathrm{AF}})=(\overrightarrow{\mathrm{BC}},\overrightarrow{\mathrm{BD}})$ est une base du plan $(\mathrm{AEF})$ mais aussi du plan $(\mathrm{BCD})$. Ces deux plans sont donc parallèles.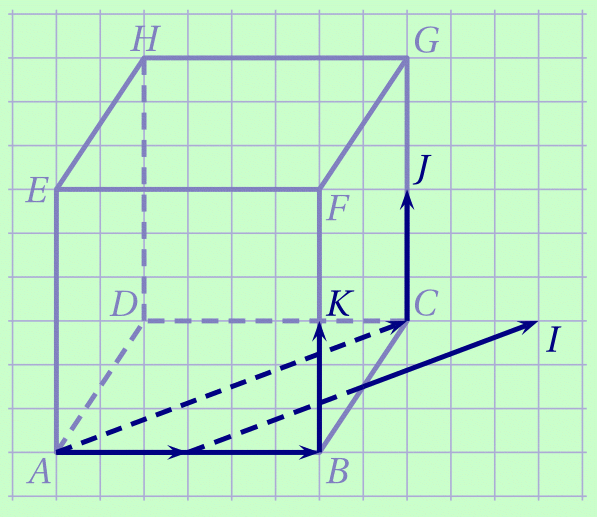
-
$\left(\overrightarrow{\mathrm{BC}},\overrightarrow{\mathrm{BD}}\right)$
est-elle une base du plan $(\mathrm{BCD})$?
retour
code : 776