retour

Soit $f$ la fonction définie sur $[-4;5]$ par la courbe $\mathscr C$ ci-dessous.

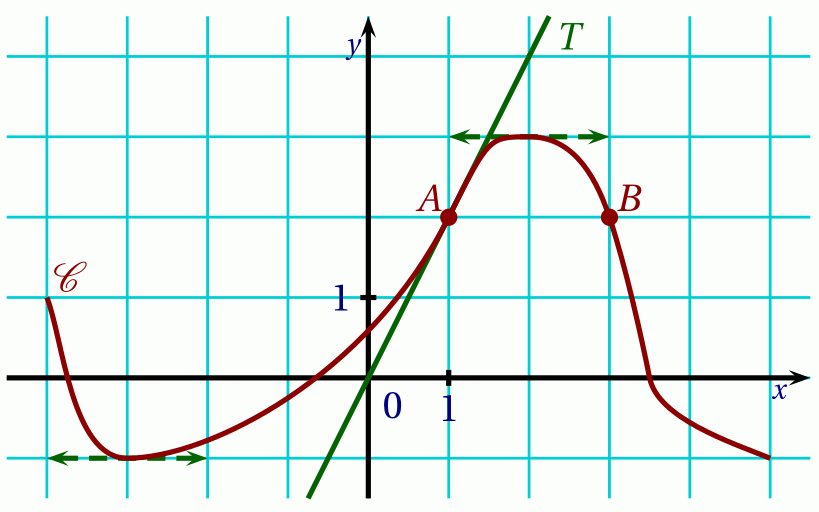
On a de plus représenté les tangentes à $\mathscr C$ aux points d'abscisses −3 et 2, ainsi que la droite $T$, tangente à $\mathscr C$ au point $A$ d'abscisse 1.

1. Donner, sans justifier, la valeur de $f(-3)$, $f(1)$, $f(2)$, $f'(-3)$, $f'(1)$ et $f'(2)$.
   Corrigé
   $f(-3)=-1$; $f(1)=2$; $f(2)=3$;
   $f'(3)$ est le coefficient directeur de la tangente à la courbe au point d'abscisse $-3$, donc $f'(-3)=0$;
   De même, $f'(1)=2$ et $f'(2)=0$.
2. Donner, toujours sans justifier, l'équation affine de la droite $T$.
   Corrigé
   La droite $T$ a pour coefficient directeur 2 et passe par l'origine donc \[T:\quad y = 2x.\]
3. Que peut-on dire du point $A$ pour la courbe $\mathscr C$? Justifier la réponse.
   Corrigé
   $T$ traverse $\mathscr C$ au point $A$. Donc $A$ est un point d'inflexion de $\mathscr C$.
4. On admet que $f'(3)=-3$. En déduire l'équation de la tangente à $\mathscr C$ au point $B(3;2)$.
   Corrigé
   Équation de la tangente au point d'abscisse 3: \begin{align*} y &= f'(3)(x-3) + f(3)& \\ \iff y &= -3(x-3)+2& \\ \iff y&=-3x + 11.& \end{align*}

retour

code : 764